Question

The diagonal of a cube is $ 30\sqrt{3} $ metres. What is the solid content?

Answer 1

Hint: Here we have been given the diagonal of the cube and we have to find the solid content in it. The solid content means the volume of the cube so firstly we will get the edge of the cube by using the formula to calculate the diagonal of the cube. Then we will substitute the edge value in the formula of the volume of the cube and simplify it to get the desired answer.

Complete step-by-step answer:
The diagonal of a cube is given as $ 30\sqrt{3} $ metres.
We know the formula to calculate the diagonal of cube is as follows:
The diagonal of cube $ =\sqrt{3}\times $ Edge
On substituting the diagonal value above we get,
 $ 30\sqrt{3}=\sqrt{3}\times $ Edge
 $ \Rightarrow \dfrac{30\sqrt{3}}{\sqrt{3}}= $ Edge
 $ \Rightarrow 30\,cm= $ Edge
So Edge $ =30\,cm $
The cub can be drawn as:

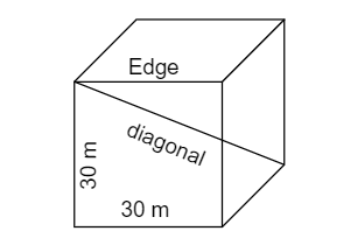
Now we have to find the solid content which means the volume.
Volume of Cube $ = $ Edge $ \times $ Edge $ \times $ Edge
Volume of cube $ =30\,cm\times 30\,cm\times 30\,cm $
Volume of cube $ =27000\,c{{m}^{3}} $
So the volume of the cube is $ 27000\,c{{m}^{3}} $
Hence the solid content of the cube with diagonal $ 30\sqrt{3} $ is $ 27000\,c{{m}^{3}} $ .
So, the correct answer is “ $ 27000\,c{{m}^{3}} $ ”.

Note: Cube is a three-dimensional figure which has $ 6 $ square faces, $ 8 $ vertices and $ 12 $ edges where the $ 3 $ edges meet at one vertex point. The edges opposite to each other are parallel. As a cube is a three-dimensional figure it contains some solid content in it which is known as the volume of the cube. There are two diagonals in a cube, one is the diagonal of the face of the cube and another is the diagonal of the cube don’t get confused in them as both of them have different formulas.