Question

The design of an iron grill is in the form of a square circumscribing a circle of radius 7 cm. Find the area between the square and the circle.

Answer 1

Hint: In this particular question first draw the pictorial representation of the given problem it will give us a clear picture of what we have to find out and square circumscribing the circle means there is a circle inside the square and the circle is touching all the sides of the square so that the diameter of the circle is equal to the side of the square so use these concepts to reach the solution of the question.

Complete step-by-step answer:

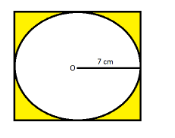
Given data:
Iron grill is in the form of a square circumscribing a circle of radius 7 cm.
Now as we all know that square circumscribing the circle means there is a circle inside the square and the circle is touching all the sides of the square so that the diameter of the circle is equal to the side of the square as shown in the above figure.
So the radius (r) of the circle is 7 cm.
Now as we know that the diameter is twice of the radius, so the diameter of the circle is
= $\left( {7 \times 2} \right)$ = 14 cm.
So, the side of the square is equal to the diameter of the circle = 14 cm.
Now as we know that the area of the circle is = $\pi {r^2}$square units, where r is the radius of the square.
So, area of the circle = $\dfrac{{22}}{7}{\left( 7 \right)^2}$, $\left[ {\because \pi = \dfrac{{22}}{7}} \right]$
So, the area of the circle = $\dfrac{{22}}{7}\left( 7 \right)\left( 7 \right) = 22\left( 7 \right) = 154$ Sq. cm.
Now as we know that the area of the square is the square of its side.
So, the area of the square is = ${\left( {{\text{side}}} \right)^2}$ sq. cm.
Now substitute the value of the side of the square we have,
So, the area of the square is = ${\left( {14} \right)^2} = 196$ sq. cm.
Now we have to find out the area between the square and the circle.
So, area between the square and the circle = area of square – area of circle.
So area between the square and the circle = $196 - 154 = 42$ Sq. cm.
So this is the required area between the square and the circle.

Note: Whenever we face such types of questions the key concept involved is the formula of the areas of square as well as of circle, so always recall the formulas which is stated above so first find out the diameter of the circle as above which is the length of the side of the square so the area between the square and the circle is the difference of the area of the square and the circle.