Question

The descending order of ${\Delta _o}$ for the following complexes will be:
(I) ${[Co{({H_2}O)_6}]^{3 + }}$
(II) ${[Co{({H_2}O)_2}{(CN)_4}]^ - }$
(III) ${[Co{({H_2}O)_4}{(CN)_2}]^ + }$
     

A. I > II > III
B. II > I > III
C. III > II > I
D. II > III > I

Answer 1

Hint: Crystal field theory (CFT) describes the breaking of degeneracies of electron orbital states, usually d or f orbitals, due to a static electric field produced by a surrounding charge distribution (anion neighbors). This theory has been used to describe various spectroscopies of transition metal coordination complexes, in particular optical spectra (colors).

Complete step by step answer:
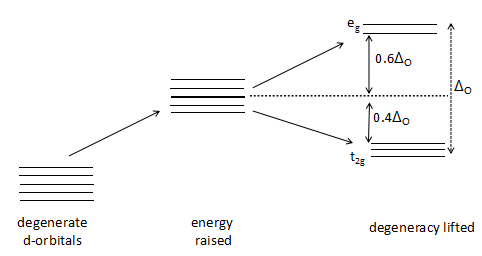
The crystal field stabilization energy (CFSE) which is denoted by ${\Delta _o}$ is the stability that results from placing a transition metal ion in the crystal field generated by a set of ligands surrounding the central metal atom/ ion. It arises due to the fact that when the d-orbitals are split in a ligand field, some of them become lower in energy than before with respect to a spherical field known as the barycenter (the point where the field is divided in the ratio of 3:2) in which all five d-orbitals are degenerate.
The greater the number of strong ligands surrounding the central metal atom, the greater the value of ${\Delta _o}$ as the pairing energy of the d- orbital electrons in the \[{t_{2g}}\] orbital is greater than the crystal field stabilization energy. The cyanide (\[C{N^ - }\] ) is a strong ligand and the greater the number of cyanide ions, the greater the CFSE of the complex. Hence, the order of the ${\Delta _o}$ in the given three complexes will be:
${[Co{({H_2}O)_2}{(CN)_4}]^ - } > {[Co{({H_2}O)_4}{(CN)_2}]^ + } > {[Co{({H_2}O)_6}]^{3 + }}$

Thus, the correct option is D. II > III > I.

Note:
In an octahedral case, the \[{t_{2g}}\] set becomes lower in energy than the orbitals in the barycenter. As a result of this, if there are any electrons occupying these orbitals, the metal ion is more stable in the ligand field relative to the barycenter by an amount known as the CFSE. Conversely, the \[{e_g}\] orbitals (in the octahedral case) are higher in energy than in the barycenter, so putting electrons in these reduces the amount of CFSE.