Question

The dependence of acceleration due to gravity $ g $ on the distance $ r $ from the centre of the Earth, assumed to be a sphere of radius $ R $ of uniform density is as shown in figures below. The correct figure is
          

          

          

          

Answer 1

Hint: We will consider the variation of value of acceleration due to gravity with the distance from the centre of the earth. Two cases can arise, one for distance from the centre is smaller than the radius of the earth and the other case is distance from the centre is larger than the radius for earth.
Formula used-
For $ R>r $ , $ g'\propto r $
For $ r>R $ , $ g'\propto \dfrac{1}{{{r}^{2}}} $

Complete step-by-step answer:
Gravitational acceleration, or the acceleration due to gravity, is defined as the free fall acceleration of a body in vacuum, without any drag force. The acceleration due to gravity is the acceleration gained by a body because of gravitational force. Its SI unit is $ m{{s}^{-2}} $ . Gravitational acceleration is a vector quantity, meaning it has both magnitude and direction.
The value of gravitational acceleration varies with altitude (height), depth, shape of earth and rotation of earth about its own axis.
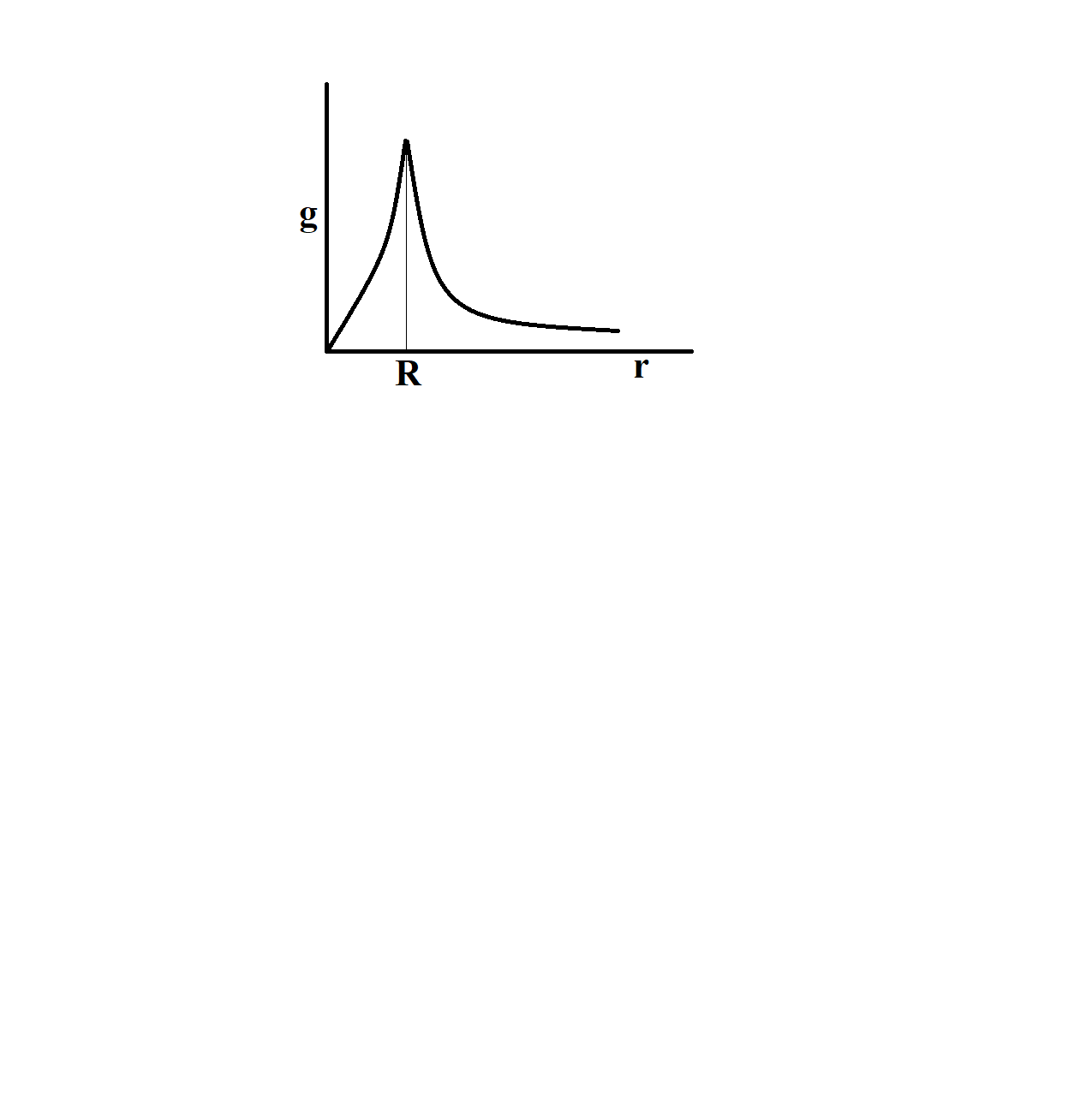
The acceleration due to gravity at a depth $ d $ below the surface of earth is given by,
 $ \begin{align}
  & g'=\dfrac{GM}{{{R}^{2}}}\left( 1-\dfrac{d}{R} \right) \\
 & g'=g\left( 1-\dfrac{d}{R} \right) \\
\end{align} $
At the centre of Earth, $ d=R $
 $ g'=0 $
At the centre of earth, acceleration due to gravity is zero.
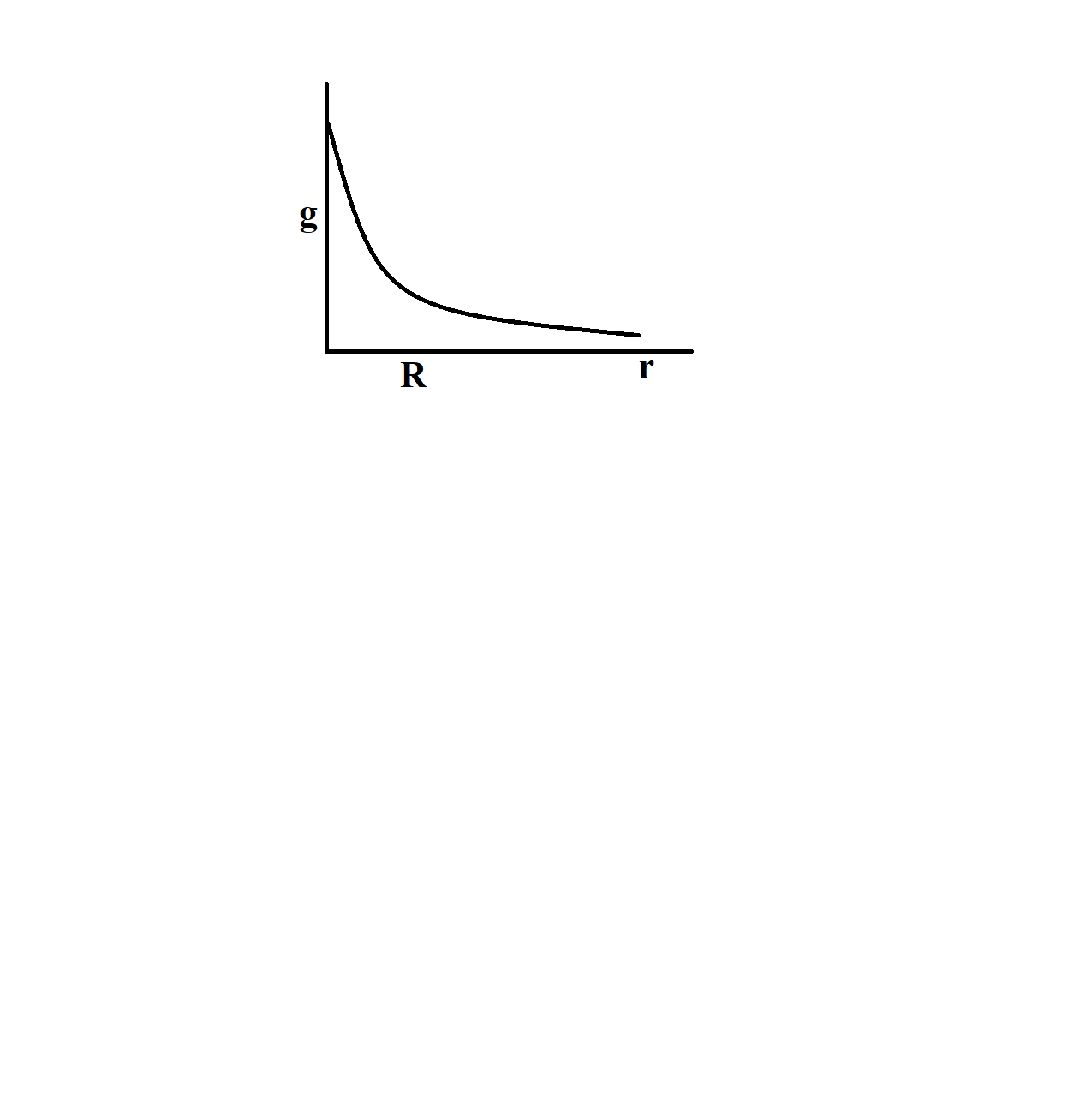
The acceleration due to gravity $ g $ varies with distance $ r $ , where $ r>R $ , is given by,
 $ \begin{align}
  & g'=\dfrac{g}{{{\left( 1+\dfrac{h}{R} \right)}^{2}}} \\
 & g'=\dfrac{g{{R}^{2}}}{{{r}^{2}}} \\
 & g'\propto \dfrac{1}{{{r}^{2}}} \\
\end{align} $
Here, $ R+h=r $
For, $ r \[\begin{align}
  & g'=g\left( 1-\dfrac{d}{R} \right) \\
 & g'=\dfrac{gr}{R} \\
 & g'\propto r \\
\end{align}\]
Here, $ R-d=r $
Thus, for $ r>R $ , we have $ g'\propto \dfrac{1}{{{r}^{2}}} $
And for For $ R>r $ , we have $ g'\propto r $
Hence, the correct option is D.

Note:
At a given place, for a fixed value of distance from the centre of earth, the value of acceleration due to gravity is constant. But the value of gravitational acceleration changes from one place to another. For an object placed at some height, the value of gravitational acceleration is less as compared to that placed on the surface of earth. As the depth increases, the value of gravitational acceleration falls.