Question

The density of ice is $ 920Kg{m^{ - 3}} $ and that of sea water is $ 1030Kg{m^{ - 3}} $ . What fraction of the total volume of an iceberg is outside the water?

Answer 1

Hint: Density is the property of substance which gives information about the mass distribution per meter cube of volume it is occupying. If the two substances of different densities come in contact the one with the lesser density will float above the one with higher density. In our case we have the density of seawater greater than ice. This means ice will float due to buoyant force.
It is an application of Archimedes' principle.
To solve we use (buoyant force = weight)
Archimedes’ principle

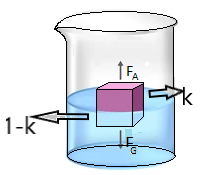
Complete answer:
 Consider the iceberg fraction visible above water as ‘k’
This means the fraction under water is $ (1 - k) $
Assuming the total volume of iceberg to be ‘V’
The volume inside water $ = V(1 - k) $
And outside water $ = kV $ .
As we know from the equilibrium of forces for an iceberg to float in that position, the weight of the iceberg should balance the buoyant force acting on it.
Si, we get
Buoyant force $ \, = {\rho _w}{V_{in}}g....(g = 10m{s^{ - 2}}) $
Weight $ = {\rho _{ice}}{V_{ice}}g $
Putting the values given in the question and assumed by us in solution,
Buoyant force $ = (1030)(1 - k)V \times (10) $
  $ = 10300(1 - k)V $
Weight $ = (920)(V)(10) $
 $ = 9200(V) $
For equilibrium,
 $ 10300(1 - k)V = 9200(V) \\
   \Rightarrow \dfrac{{103}}{{92}} = \dfrac{1}{{1 - k}} $
Reciprocating and solving we get,
 $ \dfrac{{1 - k}}{1} = \dfrac{{92}}{{103}} \\
   \Rightarrow k = 1 - \dfrac{{92}}{{103}} $
Hence,
 $ k = \dfrac{{11}}{{103}} \\
  k = 0.10 $
So 0.1 is the visible fraction or 10% iceberg is visible above water.

Note:
The buoyant force is always directed in upwards direction. The mass displaced by fluid can give the information about the mass of fluid as stated by Archimedes. The density increase will make the object sink in the object of lesser density. The more will be the density, more will be the weight of the same mass if compared with lesser densities.