
The decimal expression of \[\dfrac{1}{32}\]is ,
(a) 0.03125
(b) 0.15625
(c) 0.3125
(d) 0.00625
Answer
574.8k+ views
Hint: Divide 1 by 32 and find the quotient and remainder obtained. Check if the quotient is terminating (non-recurring) or non-terminating which is recurring. The quotient gives decimal expression.
Complete step-by-step answer:
Before going into a representation of the decimal expansion of rational numbers, let us understand what rational numbers are.
Any number that can be represented in the form of \[\dfrac{p}{q}\], such that p and q are integers and \[q\ne 0\]are known as rational numbers.
We have been given a rational number \[\dfrac{1}{32}\], which is of the form \[\dfrac{p}{q}\]where p = 1 and q =32 both are integers and \[q\ne 0\].
If we are considering other examples 7, -8.5, \[\dfrac{3}{5}\]etc are also rational numbers.
Now, let us find the decimal expansion of \[\dfrac{1}{32}\]. We know that the fraction can also be written as 1 divided by 32. Thus apply a long division method. Here 1 is the dividend and 32 is the divisor. Thus find the quotient. Insert a decimal point in the quotient, exactly above the decimal point in the number under the division bar.
Long division method involves basic mathematical operations such as multiplication, addition and subtraction, to divide two numbers. The divisor is written outside to the right, where dividend is placed inside parenthesis and the quotient is written above the over bar on the top of the dividend.
The process begins with finding how many times the leftmost digit of the dividend can be divided by the divisor. Then, the result from step - 1, which becomes the first digit of the quotient, is multiplied by the divisor and written under the first digit of the dividend. Subtraction is carried out on the first digit of the dividend and the remainder is written. The next digit of the dividend is brought down and then, the process is repeated until all the digits of the dividend are brought down and a remainder is found.
So, using long division method for \[\dfrac{1}{32}\], we get
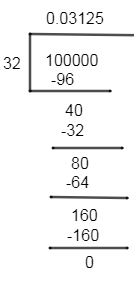
Here, the remainder is equal to zero and we got the quotient as 0.03125.
Hence we can say that the decimal form of $\dfrac{1}{32}$ is 0.03125.
Thus, the rational number \[\dfrac{1}{32}\]results in a terminating decimal.
Hence, we got the decimal expansion of \[\dfrac{1}{32}\]as 0.03125.
\[\therefore \]Option (a) is the correct answer.
So, the correct answer is “Option A”.
Note: We got the terminating decimal expansion of \[\dfrac{1}{32}\]as 0.03125. Now, if we need to convert 0.03125 back to a rational form by the following 0.03125 can be also expressed as \[\dfrac{3125}{100000}\] i.e. the decimal form can be expressed as a rational number. Now, let us simplify the rational form.
Let us divide 3125 in the numerator and denominator of \[\dfrac{3125}{100000}=\dfrac{3125\div 3125}{100000\div 3125}=\dfrac{1}{32}\].
Hence, we got the rational form as\[\dfrac{1}{32}\].
Complete step-by-step answer:
Before going into a representation of the decimal expansion of rational numbers, let us understand what rational numbers are.
Any number that can be represented in the form of \[\dfrac{p}{q}\], such that p and q are integers and \[q\ne 0\]are known as rational numbers.
We have been given a rational number \[\dfrac{1}{32}\], which is of the form \[\dfrac{p}{q}\]where p = 1 and q =32 both are integers and \[q\ne 0\].
If we are considering other examples 7, -8.5, \[\dfrac{3}{5}\]etc are also rational numbers.
Now, let us find the decimal expansion of \[\dfrac{1}{32}\]. We know that the fraction can also be written as 1 divided by 32. Thus apply a long division method. Here 1 is the dividend and 32 is the divisor. Thus find the quotient. Insert a decimal point in the quotient, exactly above the decimal point in the number under the division bar.
Long division method involves basic mathematical operations such as multiplication, addition and subtraction, to divide two numbers. The divisor is written outside to the right, where dividend is placed inside parenthesis and the quotient is written above the over bar on the top of the dividend.
The process begins with finding how many times the leftmost digit of the dividend can be divided by the divisor. Then, the result from step - 1, which becomes the first digit of the quotient, is multiplied by the divisor and written under the first digit of the dividend. Subtraction is carried out on the first digit of the dividend and the remainder is written. The next digit of the dividend is brought down and then, the process is repeated until all the digits of the dividend are brought down and a remainder is found.
So, using long division method for \[\dfrac{1}{32}\], we get
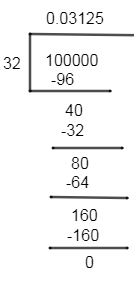
Here, the remainder is equal to zero and we got the quotient as 0.03125.
Hence we can say that the decimal form of $\dfrac{1}{32}$ is 0.03125.
Thus, the rational number \[\dfrac{1}{32}\]results in a terminating decimal.
Hence, we got the decimal expansion of \[\dfrac{1}{32}\]as 0.03125.
\[\therefore \]Option (a) is the correct answer.
So, the correct answer is “Option A”.
Note: We got the terminating decimal expansion of \[\dfrac{1}{32}\]as 0.03125. Now, if we need to convert 0.03125 back to a rational form by the following 0.03125 can be also expressed as \[\dfrac{3125}{100000}\] i.e. the decimal form can be expressed as a rational number. Now, let us simplify the rational form.
Let us divide 3125 in the numerator and denominator of \[\dfrac{3125}{100000}=\dfrac{3125\div 3125}{100000\div 3125}=\dfrac{1}{32}\].
Hence, we got the rational form as\[\dfrac{1}{32}\].
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





