Question

The daily earnings (in rupees) of 10 workers in a factory are 48, 16, 19, 8, 16, 19, 16, 8, 19, 16. The median wage is?
A. Rs.17.50
B. Rs.8.00
C. Rs.19.00
D. Rs.16.00

Answer 1

Hint: Here we arrange all the wages in ascending order or descending order so we either move higher up the scale or we move down the scale and then using the formula for median we choose the middlemost term from the observations.
* Median is the term that is exactly at the middle of the observations.
* If number of observations is odd then median is calculated by \[{\left( {\dfrac{{n + 1}}{2}} \right)^{th}}term\]
If number of observations is even then, median is calculated by \[\dfrac{{{{\left( {\dfrac{n}{2}} \right)}^{th}}term + {{\left( {\dfrac{n}{2} + 1} \right)}^{th}}term}}{2}\]
* A number is odd if it can be expressed in the form\[2n \pm 1\], example: \[5 = 2 \times 2 + 1\] is an odd number.
* A number is even if it can be expressed in the form \[2n\], example: \[18 = 2 \times 9\] is an even number.

Complete step-by-step solution:
The daily wages are 48, 16, 19, 8, 16, 19, 16, 8, 19 and 16
Total number of workers is 10
Since, these wages of workers are not in any ascending or descending order, therefore first we arrange them in ascending order (increasing order).
8, 8, 16, 16, 16, 16, 19, 19, 19, 48
Now, number of workers is 10 which is even
Therefore, using the formula for median when number of observations is even
Median \[ = \dfrac{{{{\left( {\dfrac{n}{2}} \right)}^{th}}term + {{\left( {\dfrac{n}{2} + 1} \right)}^{th}}term}}{2}\]
Substituting the value of \[n = 10\] in the formula
Median \[ = \dfrac{{{{\left( {\dfrac{{10}}{2}} \right)}^{th}}term + {{\left( {\dfrac{{10}}{2} + 1} \right)}^{th}}term}}{2}\]
\[ = \dfrac{{{{\left( 5 \right)}^{th}}term + {{\left( 6 \right)}^{th}}term}}{2}\]
Substitute the value of $5^{th}$ and $6^{th}$ term from the ascending order of wages
Now take the $5^{th}$ and $6^{th}$ term of the observations from the left side.

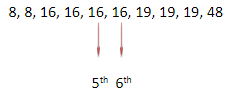
Therefore, $5^{th}$ term of the observations is 16 and $6^{th}$ term of observations is 16
Median \[ = \dfrac{{16 + 16}}{2}\]
Median \[ = \dfrac{{32}}{2}\]
Cancel same factors from numerator and denominator
Median\[ = 16\]
So, median of wages of 10 workers is Rs.16

\[\therefore \]Correct option is D.

Note: Students are likely to make mistakes in calculating the median when they have not arranged the observations in ascending or descending order. Usually students rush straight to the formula after counting the number of observations but that doesn’t work in both the cases.