Question

The curved surface area of a cone of slant height l and radius r is given by
$
  {\text{A}}{\text{. }}\dfrac{1}{3}\dfrac{\pi }{{{{\text{r}}^2}}} \\
  {\text{B}}{\text{. }}\pi {\text{rl}} \\
  {\text{C}}{\text{. }}\pi {\text{r}}{{\text{l}}^2} \\
  {\text{D}}{\text{. }}\dfrac{1}{3}\pi {\text{rl}} \\
$

Answer 1

Hint: The curved surface area of a cone is determined by the formula, curved surface area =$\left( {\dfrac{{{\text{Arc length of sector}}}}{{{\text{Circumference of circle}}}}} \right) \times {\text{Area of circle curved surface area}}$.

Complete step-by-step answer:

Given Data,
Slant height length = l and radius of the cone = r.
Now,
Curved surface area = $\left( {\dfrac{{{\text{Arc length of sector}}}}{{{\text{Circumference of circle}}}}} \right) \times {\text{Area of circle curved surface area}}$

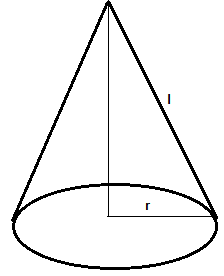
Arc length of sector = 2πr
Circumference of circle = 2πl
Area of circle curved surface area = $\pi {{\text{l}}^2}$
⟹ Curved surface area = $\left( {\dfrac{{2\pi {\text{r}}}}{{2\pi {\text{l}}}}} \right) \times \pi {{\text{l}}^2} = \pi {\text{rl}}$
Hence Option B is the correct answer.

Note: In order to solve this type of questions the key concept is to have adequate knowledge in geometrical figures like cones and circles, their properties and their formulae. Drawing an appropriate figure gives us a better idea on how to go about the problem.