Question

The curve represented by \[x=a\left( \sinh \theta +\cosh \theta \right)\] and \[y=b\left( -\sinh \theta +\cosh \theta \right)\] is
A. a hyperbola
B. a parabola
C. an ellipse
D. a circle.

Answer 1

Hint: In this problem we have to find the type of curve using the given equation. We can first write the given equation and divide a on both sides of the first equation and b on both sides of the second equation. We can then multiply the two new equations and simplify them. We will get a trigonometric identity, we can substitute the correct value of it and we will get a final equation which will represent the exact curve.

Complete step by step solution:
Here we are given two equations,
\[x=a\left( \sinh \theta +\cosh \theta \right)\]……. (1)
\[y=b\left( -\sinh \theta +\cosh \theta \right)\]……… (2)
We can now write the equation (1) as,
\[\Rightarrow \dfrac{x}{a}=\left( \sinh \theta +\cosh \theta \right)\]……. (3)
We can now write the equation (2) as,
\[\Rightarrow \dfrac{y}{b}=\left( -\sinh \theta +\cosh \theta \right)\]…….. (4)
We can now multiply equation (3) and (4), we get
\[\Rightarrow \dfrac{x}{a}\times \dfrac{y}{b}=\left( \sinh \theta +\cosh \theta \right)\times \left( -\sinh \theta +\cosh \theta \right)\]
We can now simplify the above step, we get
\[\Rightarrow \dfrac{xy}{ab}={{\cosh }^{2}}\theta -{{\sinh }^{2}}\theta \]
We know that \[{{\cosh }^{2}}\theta -{{\sinh }^{2}}\theta =1\], we can now substitute it in the above step, we get
\[\Rightarrow \dfrac{xy}{ab}=1\]
We can now multiply ab on both sides in the above step, we get
\[\Rightarrow xy=ab\]
Hence, it is a rectangular hyperbola.

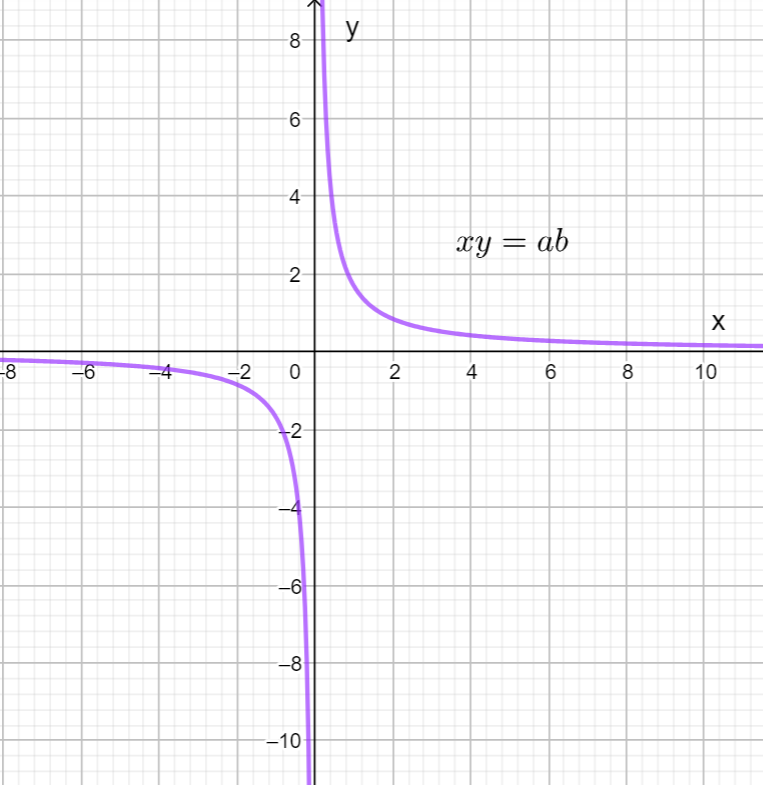
Therefore, the answer is option A. a hyperbola.

Note: We should always remember some of the trigonometric formulas and identities such as \[{{\cosh }^{2}}\theta -{{\sinh }^{2}}\theta =1\], we should also remember that the formula of a rectangular hyperbola is \[xy=ab\]. We should concentrate while multiplying the terms using the FOIL method.