Question

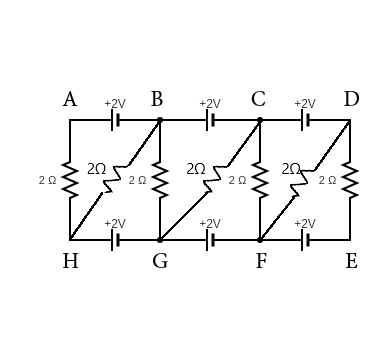
The current in branch BG is

Answer 1

Hint: To solve this problem we need to perform Kirchhoff’s voltage law around all the loops. Voltage is considered positive when moving from the negative to positive terminal for voltage sources. Voltage is subtracted when moving across a resistance in the direction of conventional current.
Formula used:
In this solution we will be using the following formula;
\[\sum V = 0\] where \[V\] is the voltage difference across the individual components.
\[\sum {{I_{in}}} = \sum {{I_{out}}} \] where \[{I_{in}}\] is the current flowing into a node, and \[{I_{out}}\] is the current flowing out the node.

Complete answer:
To solve the question, we must perform Kirchhoff’s voltage law across the loops until we can isolate the current flowing through branch BG.
Applying the voltage law to loop BAHB, we have
\[2 - 2{I_{AH}} - 2{I_{BH}} = 0\] where the subscript signifies the branch considered.
Similarly, to loop GHBG, we have
\[2 - 2{I_{BH}} - 2{I_{BG}} = 0\]
Making \[{I_{BG}}\] subject, we have
\[{I_{BG}} = 1 - {I_{BH}}\]
By subtracting this from the first loop, we have
\[2 - 2{I_{AH}} - 2{I_{BH}} - \left( {2 - 2{I_{BH}} - 2{I_{BG}}} \right) = 0\]
\[ \Rightarrow - 2{I_{AH}} + 2{I_{BG}} = 0\]
Then,
\[{I_{AH}} = {I_{BG}}\]
For loop CBGC, we have
\[2 - 2{I_{BG}} - 2{I_{GC}} = 0\]
For loop FGCF
\[2 - 2{I_{GC}} - 2{I_{CF}} = 0\]
Also, \[{I_{CF}} = 1 - {I_{GC}}\]
Subtracting from CBGC, we have
\[2 - 2{I_{GC}} - 2{I_{CF}} - \left( {2 - 2{I_{BG}} - 2{I_{GC}}} \right) = 0\]
\[{I_{CF}} = {I_{BG}}\]
For loop DCFD
\[2 - 2{I_{CF}} - 2{I_{FD}} = 0\]
For loop EFDE, we have
\[2 - 2{I_{FD}} - 2{I_{DE}} = 0\]
\[{I_{DE}} = 1 - {I_{FD}}\]
Subtracting, we have
\[2 - 2{I_{CF}} - 2{I_{FD}} - \left( {2 - 2{I_{FD}} - 2{I_{DE}}} \right) = 0\]
\[ \Rightarrow - 2{I_{CF}} + 2{I_{DE}} = 0\]
Hence,
\[{I_{CF}} = {I_{DE}}\]
At node F, we perform Kirchhoff’s current law and have that
\[{I_{EF}} = - {I_{CF}} + {I_{FG}} + {I_{FD}}\]
But \[{I_{CF}} = {I_{DE}} = 1 - {I_{FD}}\]
\[ \Rightarrow {I_{FD}} = 1 - {I_{CF}}\]
Hence, substituting into \[{I_{EF}} = - {I_{CF}} + {I_{FG}} + {I_{FD}}\], we have
\[{I_{EF}} = {I_{FG}} - 2{I_{CF}} + 1\]
Also,
\[{I_{FG}} = {I_{GH}} - {I_{BG}} + {I_{GC}}\], now as \[{I_{FD}} = 1 - {I_{CF}}\]
\[{I_{GC}} = 1 - {I_{BG}}\]
Then
\[{I_{FG}} = {I_{GH}} - 2{I_{BG}} + 1\]
Substituting into \[{I_{EF}} = {I_{FG}} - 2{I_{CF}} + 1\], we have
\[{I_{EF}} = {I_{GH}} - 2{I_{BG}} + 1 - 2{I_{CF}} + 1\]
Since, \[{I_{CF}} = {I_{BG}}\], then
\[{I_{EF}} = {I_{GH}} - 4{I_{BG}} + 2\]
Also, \[{I_{GH}} = - {I_{AH}} + {I_{BH}}\]
But \[{I_{BH}} = 1 - {I_{AH}}\], then
\[{I_{GH}} = 1 - 2{I_{AH}}\]
Inserting into \[{I_{EF}} = {I_{GH}} - 4{I_{BG}} + 2\] we have that,
Since \[{I_{AH}} = {I_{BG}}\]
\[{I_{AH}} = {I_{BG}}\]Then,
\[\begin{gathered}
  {I_{EF}} = 1 - 2{I_{BG}} - 4{I_{BG}} + 2 = 3 - 6{I_{BG}} \\
  1 - {I_{BG}} = 3 - 6{I_{BG}} \\
   \Rightarrow 6{I_{BG}} - {I_{BG}} = 3 - 2 \\
\end{gathered} \]
But \[{I_{EF}} = {I_{DE}} = {I_{CF}} = {I_{BG}}\].
Then,
\[{I_{BG}} = 3 - 6{I_{BG}}\]Solving for \[{I_{BG}}\]
\[ \Rightarrow 6{I_{BG}} + {I_{BG}} = 3\]
\[{I_{BG}} = \dfrac{3}{7} \approx 0.4{\text{A}}\]
Hence, the correct option is D.
Note: For clarity, some of the current are negative in the current law equation, because, whenever we move in the opposite direction of the assumed conventional current in the voltage law, we must make it negative. For example, for branch CF, the conventional current used in the voltage law was as though the current moved from C to F, but in the current law, it was from F to C, hence we make it negative. i.e. \[{I_{CF}} = - {I_{FC}}\]