Question

The current I in the circuit shown below is

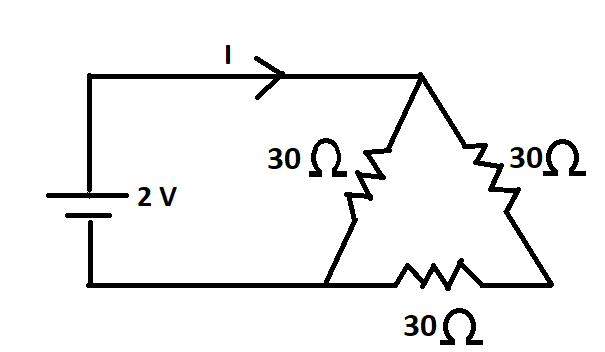
A. $\dfrac{1}{45}A$
B. $\dfrac{1}{15}A$
C. $\dfrac{1}{10}A$
D. $\dfrac{1}{5}A$

Answer 1

Hint: This is a simple circuit diagram in which resistances are in series and parallel combination, the effective resistance needs to be calculated. Then the value of current I can be calculated by using ohm's law.
Formula used:
Effective resistance in series combination:
${{R}_{s}}={{R}_{1}}+{{R}_{2}}$
Effective resistance in parallel combination:
$\dfrac{1}{{{R}_{P}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
Ohm’s Law:
$V=IR$

Complete step by step answer:

The above circuit can be simplified for solving purpose as:

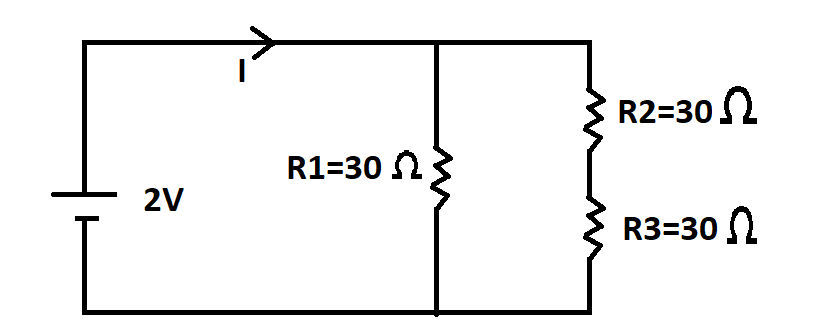
If there is only one path for current to flow in a circuit then the combination of such resistors is called a series combination and if there are more than one path for current flow in the circuit it is said to be in a parallel combination.
The two resistances on the extreme right of the circuit are in series so they can be added linearly.
${{R}_{s}}={{R}_{2}}+{{R}_{3}}$
${{R}_{s}}=30+30$
${{R}_{s}}=60\Omega $
This 60-ohm resistance is in parallel with the 30-ohm resistance, so they will be added using the formula:
$\dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{s}}}+\dfrac{1}{{{R}_{1}}}$
$\dfrac{1}{{{R}_{p}}}=\dfrac{1}{60}+\dfrac{1}{30}$
$\dfrac{1}{{{R}_{p}}}=\dfrac{1}{20}$
${{R}_{p}}=20\Omega $
Now, to calculate the current I, we use the ohm's law: The current flowing through a conductor is directly proportional to the potential difference across a conductor and temperature is constant.
$I=\dfrac{V}{R}$
Substituting the above values, we get
$I=\dfrac{2}{20}$
$I=\dfrac{1}{10}A$
Thus, the correct answer is option C. $\dfrac{1}{10}A$

Note: Students must remember that for solving questions with complicated closed network circuits Kirchhoff’s Laws can be used since ohm’s law is hard to apply .In a circuit if the resistances are connected in series then the current across each resistor is same and when the resistances are in parallel combination the voltage across each resistor remains the same.