Question

The current I in the circuit shown below is:
A) 1A.
B) 2.25A.
C) 0.5A.
D) Zero.

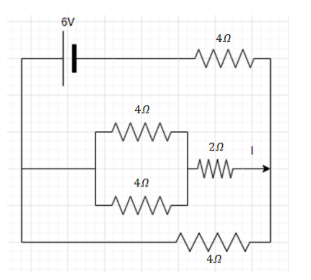
Answer 1

Hint:The Kirchhoff’s Voltage Law is the Kirchhoff’s second law that states that the energy is conserved around a closed circuit path. The parallel and series combination of resistance can be used to simplify the circuit.

Formula used:The formula of the ohm's law is given by,
$ \Rightarrow V = I \times R$
Where potential difference is V, the current is I and the resistance is R.
The formula of the parallel combination resistance is given by,

$ \Rightarrow \dfrac{1}{{{r_{eq.}}}} = \dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}}$

Where the equivalent resistance is ${r_{eq.}}$and ${r_1}$, ${r_2}$ are resistors which are in parallel combination.
The formula of the series combination resistance is given by,

$ \Rightarrow {r_{eq.}} = {r_1} + {r_2}$

Where equivalent resistance is ${r_{eq.}}$ and the resistors in series combination are ${r_1}$ and ${r_2}$.

Complete step by step solution:
It is given in the problem that the circuit diagram is given and we need to find the current I in the given circuit.
First of all we will solve the parallel resistance.

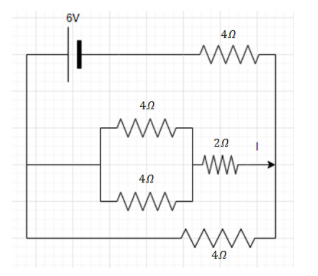
As the both $4\Omega $ resistance are in parallel combination.
The parallel combination is solved as follows,

$ \Rightarrow \dfrac{1}{{{r_{eq.}}}} = \dfrac{1}{4} + \dfrac{1}{4}$
$ \Rightarrow \dfrac{1}{{{r_{eq.}}}} = \dfrac{2}{4}$
$ \Rightarrow \dfrac{1}{{{r_{eq.}}}} = \dfrac{1}{2}$
$ \Rightarrow {r_{eq.}} = 2\Omega $.

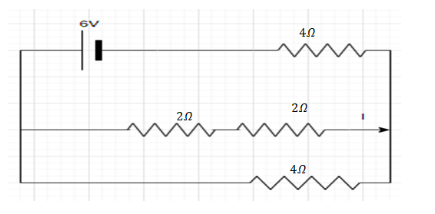
Now we will solve the resistance in series,
The resistance in series combination can be solved as,

$ \Rightarrow {r_{eq.}} = \left( {2 + 2} \right)\Omega $
$ \Rightarrow {r_{eq.}} = 4\Omega $

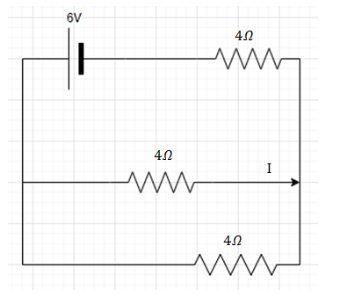
Applying the Kirchhoff’s Voltage Law rule in the two circuits we get,

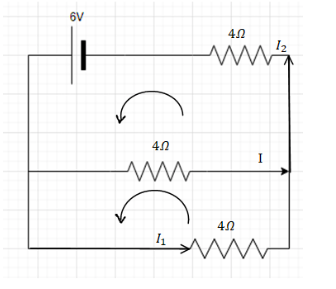
The currents which are

$ \Rightarrow {I_2} = I + {I_1}$………eq. (1)

Solving the upper circuit we get,

$ \Rightarrow 6 - 4I - 4{I_2} = 0$………eq. (2)

Solving the lower circuit we get.

$ \Rightarrow 4I = 4{I_1}$
$ \Rightarrow {I_1} = I$.........eq. (3)

Replacing the equation (3) in equation (1) we get,

$ \Rightarrow {I_2} = I + {I_1}$
$ \Rightarrow {I_2} = I + I$
$ \Rightarrow {I_2} = 2I$………eq. (4)

Replacing the value of equation (4) in equation (2) we get,

$ \Rightarrow 6 - 4I - 4{I_2} = 0$
$ \Rightarrow 6 - 4I - 4\left( {2I} \right) = 0$
$ \Rightarrow 6 - 4I - 8I = 0$
$ \Rightarrow 6 - 12I = 0$
$ \Rightarrow I = 0 \cdot 5A$.

The current I is equal to $I = 0 \cdot 5A$.

Note:The ohm's law states the relation between the potential difference, resistance and the current. The students are advised to understand and remember the concept of Kirchhoff’s Voltage law as it is very helpful in solving problems like these.