Question

The current flowing through the segment $AB$ of the circuit shown in figure is

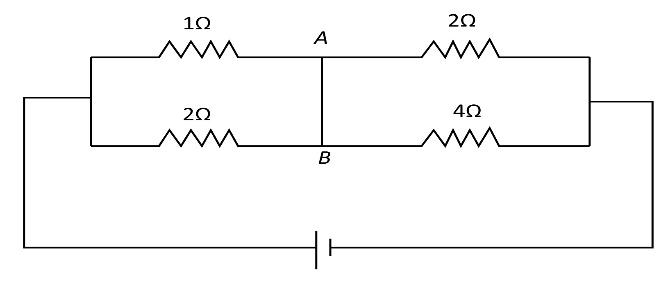
(A) $1\;{\rm{amp}}$ from $A$ to $B$
(B) $1\;{\rm{amp}}$ from $B$ to $A$
(C) $2\;{\rm{amp}}$ from $A$ to $B$
(D) $2\;{\rm{amp}}$ from $B$ to $A$

Answer 1

Hint: First, we can redraw the circuit diagram so that it is easy to identify the parallel resistances and the resistances in series with each other. We can apply the current divider rule to the circuit to find the solution.

Complete step by step answer:Let us first redraw the given circuit diagram as follows:

Here the points $A$ and $B$ are joined using a metal wire. Hence, the potential difference across the points $A$ and $B$ is zero. Thus

Let us define ${R_1} = 1\;\Omega $, ${R_2} = 3\;\Omega $, ${R_3} = 2\;\Omega $ and ${R_4} = 4\;\Omega $. From the circuit diagram, the resistances ${R_1}$ and ${R_2}$ are connected parallel to each other. Similarly, the resistances ${R_3}$ and ${R_4}$ are connected parallel to each other.

The equivalent resistance of the resistances ${R_1}$ and ${R_2}$ can be written as

${R_{1,2}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$

Here ${R_{1,2}}$ is the equivalent resistance of the resistances ${R_1}$ and ${R_2}$.

Substituting the values for ${R_1}$ and ${R_2}$ in the above equation, we get

\begin{align*}
{R_{1,2}} &= \dfrac{{1\;\Omega \times 3\;\Omega }}{{1\;\Omega + 3\;\Omega }}\\
 \Rightarrow {R_{1,2}} &= \dfrac{3}{4}\;\Omega
\end{align*}

Again, we can write the equation for the equivalent resistance of the resistances ${R_3}$ and ${R_4}$ as

${R_{3,4}} = \dfrac{{{R_3}{R_4}}}{{{R_3} + {R_4}}}$

Here ${R_{3,4}}$ is the equivalent resistance of the resistances ${R_3}$ and ${R_4}$.

Substituting the values for ${R_3}$ and ${R_4}$ in the above equation, we get

\begin{align*}
{R_{3,4}} &= \dfrac{{2\;\Omega \times 4\;\Omega }}{{2\;\Omega + 4\;\Omega }}\\
 \Rightarrow {R_{3,4}} &= \dfrac{{8\;{\Omega ^2}}}{{6\;\Omega }}\\
 \Rightarrow {R_{3,4}} &= \dfrac{4}{3}\;\Omega
\end{align*}

From the circuit diagram we can see that the combination of parallel resistances ${R_1}$ and ${R_2}$ is in series with the combination of parallel resistances ${R_3}$ and ${R_4}$. Hence, we can write the equation for the equivalent resistance of the four resistances as,

$R = {R_{1,2}} + {R_{3,4}}$

Here $R$ is the equivalent resistance of the four resistances.

Now, we can substitute $\dfrac{3}{4}\;\Omega $ for ${R_{1,2}}$ and $\dfrac{4}{3}\;\Omega $ for ${R_{3,4}}$ in the above equation to get,

\begin{align*}
R &= \dfrac{3}{4}\;\Omega + \dfrac{4}{3}\;\Omega \\
 \Rightarrow R &= \left( {\dfrac{{3 \times 3 + 4 \times 4}}{{4 \times 3}}} \right)\;\Omega \\
 \Rightarrow R &= \dfrac{{25}}{{12}}\;\;\Omega
\end{align*}

Now the total current flowing through the circuit can be written as

$I = \dfrac{V}{R}$

Here $V$ is the voltage across the circuit.

Since $V = 25\;{\rm{V}}$ and $R = \dfrac{{25}}{{12}}\;\Omega $, we can substitute the values for $R$ and $V$ to get the total current. Hence,

\begin{align*}
I &= \dfrac{{25\;{\rm{V}}}}{{\dfrac{{25}}{{12}}\;\Omega }}\\
 \Rightarrow I &= 12\;{\rm{A}}
\end{align*}

Now, using the current divider rule, we can write the equation for the current ${I_1}$ flowing between point $P$ to $A$ as,

${I_1} = \dfrac{{{R_2}}}{{{R_1} + {R_2}}}I$

Substituting the values for ${R_1}$, ${R_2}$ and $I$ in the above equation, we get

\begin{align*}
{I_1} &= \dfrac{{3\;\Omega }}{{1\;\Omega + 3\;\Omega }} \times 12\;{\rm{A}}\\
 \Rightarrow {I_1} &= \dfrac{3}{4} \times 12\;{\rm{A}}\\
 \Rightarrow {I_1} &= 9\;{\rm{A}}
\end{align*}

Again, using the current divider rule, we can write equation for the current ${I_3}$ flowing from point $B$ to $Q$ as,

${I_3} = \dfrac{{{R_3}}}{{{R_3} + {R_4}}}I$

Substituting the values for ${R_3}$, ${R_4}$ and $I$ in the above equation, we get

\begin{align*}
{I_3} &= \dfrac{{4\;\Omega }}{{2\;\Omega + 4\;\Omega }} \times 12\,{\rm{A}}\\
 \Rightarrow {I_3} &= \dfrac{4}{6} \times 12\,{\rm{A}}\\
 \Rightarrow {I_3} &= 8\;{\rm{A}}
\end{align*}

Now, the current flowing through the segment $AB$ can be written as

$i = {I_1} - {I_3}$

Here $i$ is the current flowing through the segment $AB$.

Now substituting the values of ${I_1}$ and ${I_3}$, we get

\begin{align*}
i &= 9\;{\rm{A - 8}}\;{\rm{A}}\\
 \Rightarrow i &= 1\;{\rm{A}}
\end{align*}

Since, the current obtained has a positive value, we can confirm that the direction of the current is from $A$ to $B$.

Therefore, the option (A) is correct.

Note:It should be noted that the resistances connected between two pints at the same potential difference are in parallel. Similarly, we should also note that the resistances connected between points at different potential differences are in series.