Question

The cross-section of a bar is given by $\left( 1+\dfrac{{{X}^{2}}}{100} \right)c{{m}^{2}}$, where X (in cm) is the distance from one end. Find the extension under a load of $20kN$ at the other end at a length of 10cm. $\left( y=2\times {{10}^{5}}N/m{{m}^{2}} \right)$.

Answer 1

Hint: In this question the cross sectional area is changing along the length so to solve this question. We will consider a small part of the rod and take integration along the given length to find the relevant solution.

Formula used:
$\begin{align}
  & Y=\dfrac{\sigma }{\varepsilon } \\
 & \sigma =\dfrac{F}{A} \\
 & \varepsilon =\dfrac{\sigma }{l} \\
\end{align}$

Complete step by step solution:

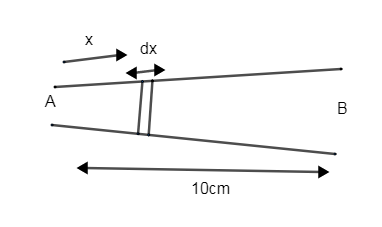
Let’s assume that the total extension of the rod is given as $\Delta l$.
Now let’s consider small part dx with a cross section of $\left( 1+\dfrac{{{x}^{2}}}{100} \right)c{{m}^{2}}$.

Now stress on this small part dx is,
$\Rightarrow \sigma =\dfrac{F}{A}...\left( 1 \right)$
Where, σ = stress on dx
F = total force on the rod
A = cross sectional area.

Now strain on the small dx part,
$\varepsilon =\dfrac{dl}{dx}...(2)$
Where, dx = actual length
dl = change in the length
ε = strain in small part dx
Now formula of the young’s modulus,
$Y=\dfrac{\sigma }{\varepsilon }....\left( 3 \right)$

Now substitute value of the equation (1) and (2) in the equation (3)
$\begin{align}
  & \Rightarrow Y=\dfrac{F}{A}\times \dfrac{dx}{dl} \\
 & \Rightarrow dl=\dfrac{F}{AY}dx...(4) \\
\end{align}$

Now the value are given as,
$\begin{align}
  & F=20kN \\
 & =20\times {{10}^{3}}N \\
 & A=\left( 1+\dfrac{{{x}^{2}}}{100} \right) \\
 & Y=2\times {{10}^{5}}N/m{{m}^{2}} \\
 & =2\times {{10}^{7}}N/c{{m}^{2}} \\
 & \left( \because N/m{{m}^{2}}\to N/c{{m}^{2}} \right) \\
\end{align}$

Now substitute all the values in the equation (4)
$\begin{align}
  & \Rightarrow dl=\dfrac{20\times {{10}^{3}}}{\left( 1+\dfrac{{{x}^{2}}}{100} \right)\times 2\times {{10}^{7}}} \\
 & \Rightarrow dl=\dfrac{{{10}^{-3}}\times dx}{\left( 1+\dfrac{{{x}^{2}}}{100} \right)} \\
\end{align}$

Now let’s take the integration on the both sides,
$\Rightarrow \int{dl}=\int\limits_{0}^{10}{\dfrac{{{10}^{-3}}\times dx}{\left( 1+\dfrac{{{x}^{2}}}{100} \right)}}$

Here we taken limit as 0 to 10 because total length is 10cm,
$\begin{align}
  & \Rightarrow \Delta l={{10}^{-3}}\int\limits_{0}^{10}{\dfrac{dx}{1+\dfrac{{{x}^{2}}}{{{10}^{2}}}}} \\
 & \Rightarrow \Delta l={{10}^{-3}}\int\limits_{0}^{10}{\dfrac{dx}{1+{{\left( \dfrac{x}{10} \right)}^{2}}}} \\
\end{align}$

Here we will apply formula as shown,
$\Rightarrow \int{\dfrac{dt}{1+{{t}^{2}}}}={{\tan }^{-1}}t+C$

Applying the formula,
\[\begin{align}
  & \Rightarrow \Delta l={{10}^{-3}}\left( \dfrac{1}{\dfrac{1}{10}}{{\tan }^{-1}}\dfrac{x}{10} \right)_{0}^{10} \\
 & \Rightarrow \Delta l={{10}^{-3}}\times 10\left( {{\tan }^{-1}}\left( 1 \right)-{{\tan }^{-1}}\left( 0 \right) \right) \\
 & \Rightarrow \Delta l={{10}^{-2}}\left( \dfrac{\pi }{4}-0 \right) \\
 & \therefore \Delta l=0.78\times {{10}^{-2}}cm \\
\end{align}\]

Therefore extension under a load of 20kN is \[0.78\times {{10}^{-2}}cm\].

Note:
When we are substituting values be remember to convert all the values in the same unit similar to the solution that we see above. Additionally, note that whenever any body is subjected to a force which results in the change of its dimensions, but regardless of those changes the volume of the body remains the same.