Question

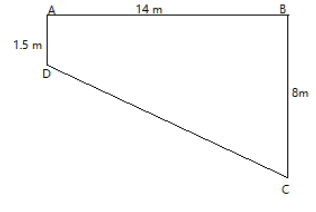
The cross-section \[ABCD\] of a swimming pool is a trapezium. It's width \[AB = 14{\text{m}}\] depth at the shallow end is 1.5 m and at the deep end is 8 m. Find the area of the cross-section.

Answer 1

Hint: Construct the line \[DE\] perpendicular to the line \[BC\]. Find the area of the triangle \[DCE\] using the formula \[\dfrac{1}{2} \times base \times height\]. Find the area of the rectangle \[DABE\] using the formula \[Base \times height\]. Add the two to find the answer.

Complete step-by-step answer:

We will first construct the line \[DE\] perpendicular to the line \[BC\]. \[E\] is the intersection point of \[BC\]and $DE$, such that $BC \bot DE$

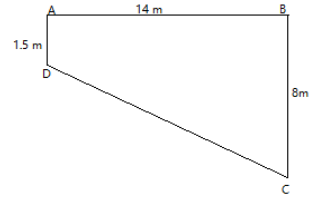
We know that the area of the triangle is \[\dfrac{1}{2} \times base \times height\]. In the triangle \[DCE\], the area can be calculated by substituting \[DE\] for base and \[CE\].
\[\dfrac{1}{2} \times CE \times DE\]
From the figure it is evident that, \[DE = AB = 14{\text{m}}\] and, \[CE + EB = {\text{ }}8{\text{m}}\]. Also, \[AD = EB = 1.5{\text{m}}\]
Therefore \[CE = 8 - 1.5 = 6.5{\text{m}}\].
Substituting the value 6.5 for \[CE\] and 14 for \[DE\] in the equation \[\dfrac{1}{2} \times CE \times DE\].
Thus, area of the triangle \[DCE\] = \[\dfrac{1}{2} \times 6.5 \times 14 = 45.5{{\text{m}}^3}\]

Also, the area of the rectangle is given by the formula \[Base \times height\].
Substituting the value of base with \[AB\] and \[AD\] for height in the formula \[Base \times height\] to find the area of the rectangle \[ABED\].
Area of \[ABED\]=\[AB \times AD\].
Substituting the value 14 for \[AB\] and 1.5 for \[AD\], we get
Area of \[ABED\]= \[14 \times 1.5 = 21\]
The area of the cross-section \[ABCD\] is equal to the sum of the section \[ABED\] and section \[DCE\].
Area of \[ABCD\]= Area of \[ABED\]+ Area of \[DCE\].
Area of \[ABCD\]= $45.5 + 21 = 66.5{{\text{m}}^3}$
Thus the area of the cross section \[ABCD\] is \[66.5{{\text{m}}^3}\].

Note: The formula of the area of the trapezium can also be used alternatively. The area of the trapezium is given by \[\dfrac{1}{2} \times \left( {sum{\text{ }}of{\text{ }}the{\text{ }}parallel{\text{ }}sides} \right) \times {\text{ }}height{\text{ }}between{\text{ }}the{\text{ }}parallel{\text{ }}sides\].