Question

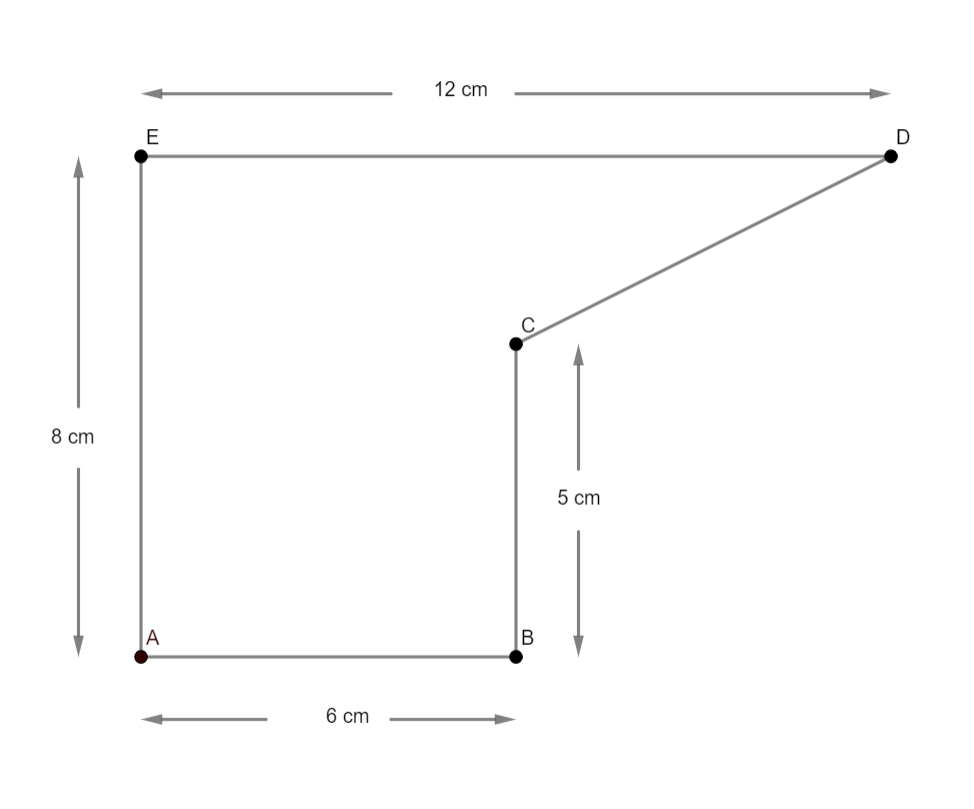
The cross section of a piece of metal $2{\text{ cm}}$ in length is shown in the figure given below. Calculate
i. The area of cross section
ii The volume of the piece of metal in cubic centimeters ($c{m^3}$). If $1{\text{ c}}{{\text{m}}^3}$ of the metal weighs $6.6{\text{ gm}}$, calculate the weight of the piece of metal to the nearest kg.

Answer 1

Hint: We have to calculate the area of the cross-section, and also the volume of the piece of the metal along with the weight of the metal. First we will break this area into some parts and then calculate the area of the cross section. Then we will use the length of the metal given to us to find the volume and consequently the area of the cross section.

Complete step by step answer:
Let us break the cross section into two pieces, one will be the rectangle of sides, $8{\text{ cm and 6 cm}}$. The other part being a right angled triangle whose sides are ${\text{3 cm and 6 cm}}$.

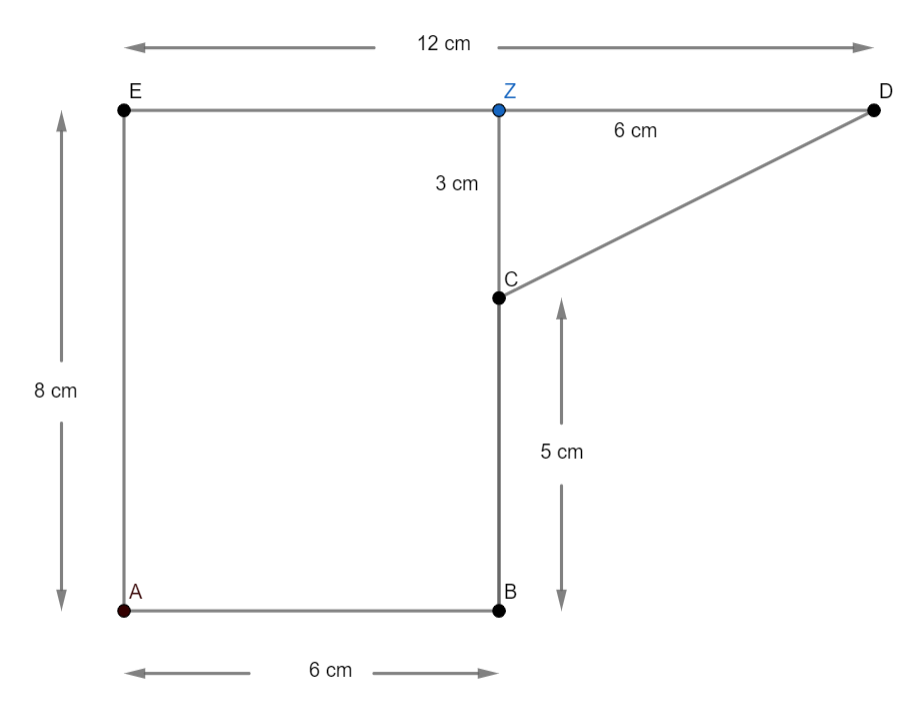
Area of the rectangle (EABZ):
$Area = Length \times Breadth$
$Area = 8 \times 6$
$Area = 48{\text{ c}}{{\text{m}}^2}$
Area of the Right angled triangle : (CZD)
$Area = \dfrac{1}{2} \times Base \times Perpendicular$
$Area = \dfrac{1}{2} \times 3 \times 6$
$Area = 9{\text{ c}}{{\text{m}}^2}$
The total area of cross section is therefore $48 + 9 = 57{\text{ c}}{{\text{m}}^2}$
Volume will be calculated by multiplying this area by the length of the metal which is given as $2{\text{ m}}$, converting it into centimetres we get,
$2{\text{m }} = {\text{ 200 cm}}$
Volume will then be calculated as:
$V = 57 \times 200$
$V = 11400{\text{ c}}{{\text{m}}^3}$
Thus volume is calculated.
Now to find the weight :
Multiplying volume by density we get,
$W = 11400 \times 6.6$
$W = 75240{\text{ gm}}$
Converting this to kilogram we get,
$W = 75.240{\text{ kg}}$ rounding off to the nearest kg we get,
$W = 75kg$
Thus the weight of the metal is $75{\text{ kg}}$.

Note:
1. The formula for density is given by:
$Density = \dfrac{{mass}}{{volume}}$
We have just rearranged the formula to use it above to find the weight (mass ) as:
$mass = Density \times Volume$
2. Volume of a solid when area of the cross-section and length is given:
$\text{Volume = Area of cross section} \times \text{Length}$
3. We have used this formula above to find the volume of the metal.
The cross-section in the above case could have been broken into the form of trapezium as well but that would have made the question difficult and students should try to break irregular areas into rectangles and triangles for simplicity of the solution.