Question

The cost of painting the total surface area of cones at 25 paise per $ \text{c}{{\text{m}}^{2}} $ is Rs 176. Find the volume of the cone, if its slant height is 25cm. \[\]

Answer 1

Hint: We find the total surface area by dividing total cost by cost per unit area. We recall the total surface with slant height $ l $ and radius of the base $ r $ as $ \pi {{r}^{2}}+\pi rl $ . We put the given value $ l=25 $ and equate to the obtained surface area to get a quadratic equation in $ r $ which we solve to get $ r $ . We find the required volume $ V=\pi {{r}^{2}}h $ . \[\]

Complete step by step answer:
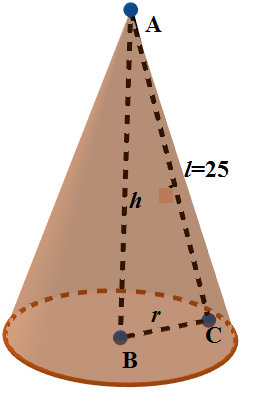
We have drawn the figure of the given right circular cone above with apex A and the centre of circular base B and C a point on the circular base. The line segment joining the apex to the centre is the height of the cone denoted as $ h $ and the line segment joining the apex to any point the circular base is called slant height and denoted as $ l $ . The surface made by the slant height is called the curved surface of the cone. The total surface area with radius at the base $ r $ is given by
\[\text{TSA}=\pi {{r}^{2}}+\pi rl........\left( 1 \right)\]
The volume of the cone is given by
\[V=\pi {{r}^{2}}h=\pi {{r}^{2}}\sqrt{{{l}^{2}}-{{r}^{2}}}\]
We give in the question that the cost of painting the total surface area of cone at 25 paisa per $ \text{c}{{\text{m}}^{2}} $ is Rs 176 and the slant height is $ l=25 $ cm.
So the total surface area is
\[\text{TSA=}\dfrac{\text{total cost}}{\text{cost per c}{{\text{m}}^{2}}}=\dfrac{176}{0.25}=704\text{ c}{{\text{m}}^{2}}.......\left( 2 \right)\]
We put $ l=25 $ cm and equate the right hand sides of equation (1) and (2) to have;
\[\begin{align}
  & \Rightarrow \pi {{r}^{2}}+\pi r\times 25=704 \\
 & \Rightarrow \pi \left( {{r}^{2}}+25r \right)=704 \\
 & \Rightarrow {{r}^{2}}+25r=\dfrac{704}{\pi }=704\times \dfrac{7}{22}=224 \\
 & \Rightarrow {{r}^{2}}+25r-224=0 \\
\end{align}\]
The above equation is a quadratic equation in $ r $ which we solve by splitting the term $ 25r $ . W have;
\[\begin{align}
  & \Rightarrow {{r}^{2}}+32r-7r-224=0 \\
 & \Rightarrow r\left( r+32 \right)-7\left( r+32 \right)=0 \\
 & \Rightarrow \left( r+32 \right)\left( r-7 \right)=0 \\
 & \Rightarrow r+32=0\text{ or }r-7=0 \\
\end{align}\]
So we have two solutions to the quadratic equation $ r=-32,7 $ . We reject $ r=-32 $ since length cannot be negative and hence conclude $ r=7 $ cm. We use the formula for volume of a cone and find the required volume with
\[V=\dfrac{1}{3}\pi {{r}^{2}}\sqrt{{{l}^{2}}-{{r}^{2}}}=\dfrac{1}{3}\dfrac{22}{7}\times 7\times 7\times \sqrt{{{25}^{2}}-{{7}^{2}}}=\dfrac{1}{3}\times 22\times 7\times 24=528\text{ c}{{\text{m}}^{3}}\]

Note:
 We must be careful that the painting cost per unit $ \text{c}{{\text{m}}^{2}} $ is given paisa and the total cost is given rupees. So we need to convert into the same unit before division. The relation $ h=\sqrt{{{l}^{2}}-{{r}^{2}}} $ can be obtained using Pythagoras theorem in triangle ABC. The total surface area is the sum of curved surface area $ \left( \pi rl \right) $ and the area at circular base $ \left( \pi {{r}^{2}} \right) $ . We can find the factor for splitting the middle term while solving the quadratic equation from prime factorization of 224.