Question

The cost of carpeting a room is Rs. 120. If the width had been 4 metres less, the cost of the carpet would have been Rs. 20 less. The width of the room is \[\]
A.24m\[\]
B.20m\[\]
C.18m\[\]
D. 18.5m \[\]

Answer 1

Hint: We recall the area of the rectangle as the product of length$l$ (also called width) and breadth $b$ of the rectangle. The room is rectangular and hence the carpet will be rectangular. We assume cost as area of the area of rectangle and design equations using the given data $lb=120,\left( l-4 \right)b=100$ . We solve for $l$.

Complete step-by-step answer:
We know that carpets are made in different forms and the cost of making a carpet is calculated on the area of the carpet. We also know that the area of the rectangle is the product of length (also called width) and breadth of the rectangle.\[\]

We are given the question that the cost of carpeting a room is Rs. 120. Since we have to cover a rectangular room, the carpet will also be made in rectangular form. Let us assume the length of the rectangular carpet as $l$metre and the width of rectangular carpet as $b$metre. We can represent the cost rs.120 as the area in ${{m}^{2}}$. So we have;
\[\begin{align}
  & l\times b=120 \\
 & \Rightarrow b=\dfrac{120}{l}....\left( 1 \right) \\
\end{align}\]

We are further given in the question that If the width had been 4 metres less, the cost of the carpet would have been Rs. 20 less.

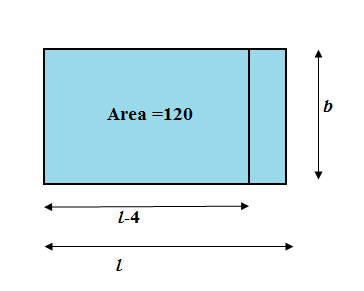
So the new width is $\left( l-4 \right)$m and the new area is $120-20=100{{\text{m}}^{2}}$ but the breadth is the same $b$. We have,
\[b\left( l-4 \right)=100\]
We put the value of $b$ from equation and put in above equation to have;
\[\Rightarrow \dfrac{120}{l}\left( l-4 \right)=100\]
We multiply both sides by $b$ to have;
\[\Rightarrow 120\left( l-4 \right)=100l\]
We divide both side of the equation by 20 to have;
\[\begin{align}
  & \Rightarrow 6\left( l-4 \right)=5l \\
 & \Rightarrow 6l-24=5l \\
 & \Rightarrow 6l-5l=24 \\
 & \Rightarrow l=24 \\
\end{align}\]
So the width of the carpet is 24m. Hence the correct choice of the question is A.

So, the correct answer is “Option A”.

Note: We must be careful that the cost of the carpet is calculated on the area not on the perimeter of the carpet $2\left( l+b \right)$. Here we have assumed the cost per unit area that is per ${{\text{m}}^{2}}$ as one rupee. We can find breath of the carpet and room as $b=\dfrac{120}{l}=\dfrac{120}{24}=5$m.