Question

The cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs. 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs. 300. Represent the situation algebraically and graphically.
A. \[\begin{align}
  & 2x+y=160\text{ } \\
 & 4x+2y=300 \\
\end{align}\]
B. \[\begin{align}
  & x+2y=160\text{ } \\
 & 4x+2y=300 \\
\end{align}\]
C. \[\begin{align}
  & x+2y=160\text{ } \\
 & 2x-4y=300 \\
\end{align}\]
D. None of these

Answer 1

Hint: Find the equations from the given conditions to represent the situation algebraically. Then plot the two curves of those two equations to represent the situation graphically. Assume that the cost of 1 kg of apples is Rs. x and 1 kg grapes is Rs. y . There will be two different equations from the two given conditions.

Complete step-by-step answer:
In the question, we are given that the cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs. 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs. 300.
So here to represent the two situations algebraically, we have to find two equations in terms of the two variables x and y. Now here assume that the cost of 1 kg of apples is Rs. x and 1 kg grapes is Rs. y .
So here, in situation 1, it is given that the cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs. 160. So the cost of 2 kg of apples is given as Rs 2x and the cost of 1 kg of grapes is Rs y.
Also, the total is Rs 160, so in the equation form, we will get: \[2x+y=160\text{ }\].
Again, it is given that the cost of 4 kg of apples and 2 kg of grapes is Rs. 300. So the cost of 4 kg of apples is given as Rs 4x and the cost of 2 kg of grapes is Rs 2y.
Now again here the total is Rs 300, so in the equation form, we will get: \[4x+2y=300\].
So combining the two situations, we get:
\[\begin{align}
  & 2x+y=160\text{ } \\
 & 4x+2y=300 \\
\end{align}\]
And hence this is the algebraic representation.
Hence Option A is correct.

Now, for the graphical representation, we need to use the graphic utility and will plot the two equations as shown below:

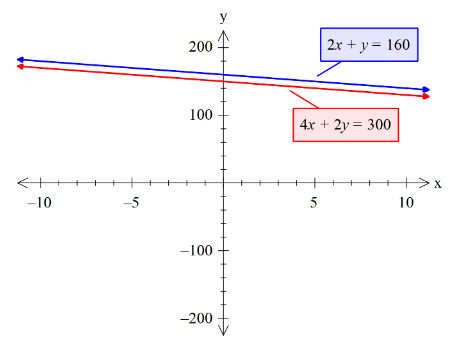
So here the red curve is \[4x+2y=300\] and the blue curve is \[2x+y=160\text{ }\]

Note: Care has to be taken while simplifying the finding the total cost. Here, we are not required to find the cost of apples and grapes but just have to represent the situation algebraically and graphically. The two lines are parallel and hence do not have intersection points.