
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs.160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs.300. Represent the situation algebraically and geometrically.
Answer
585.3k+ views
Hint: In this question, we need to assume the cost of kg apples as x and the cost of kg grapes as y. Then from the given conditions in the question, we get the respective algebraic equations which then on converting in terms of any of the one variable helps in geometric representation.
Complete step by step answer:
Let us assume the cost of 1 kg apples as Rs. x and the cost of 1 kg grapes as Rs. y
Now, given that the cost of 2 kg apples and 1 kg grapes is Rs.160
Now, this can be written in terms of the algebraic equation as
\[\Rightarrow 2x+y=160\]
Now, given that the cost of 4 kg apples and 2 kg grapes is Rs.300
Now, this can be written in terms of the algebraic equation as
\[\Rightarrow 4x+2y=300\]
Now, the algebraic representation of the given system is
\[\begin{align}
& 2x+y=160 \\
& 4x+2y=300 \\
\end{align}\]
Now, let us write the above both equations in terms of y
\[\Rightarrow y=160-2x\]
\[\Rightarrow y=\dfrac{300-4x}{2}\]
Now, let us find few corresponding values to represent them geometrically
Now, plot these points to represent the situation geometrically
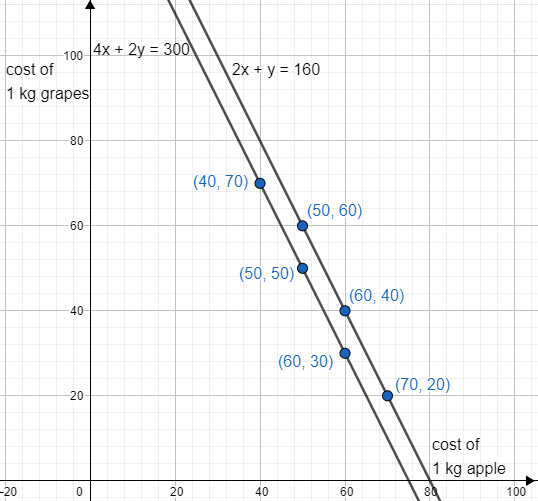
Here, we can observe that both the lines do not intersect each other and are parallel so they do not have a common solution which means they have no unique solution.
This shows the prices are different
Note:
Instead of finding the equations in terms of y to represent them geometrically, we can also express them in terms of x and they further consider the values respectively and then represent which also gives the same representation.
It is important to note that the two lines are parallel which means they have a trivial solution and no unique solution. It is also to be noted that while writing the equations we should not neglect any of the terms which change the corresponding equation.
Complete step by step answer:
Let us assume the cost of 1 kg apples as Rs. x and the cost of 1 kg grapes as Rs. y
Now, given that the cost of 2 kg apples and 1 kg grapes is Rs.160
Now, this can be written in terms of the algebraic equation as
\[\Rightarrow 2x+y=160\]
Now, given that the cost of 4 kg apples and 2 kg grapes is Rs.300
Now, this can be written in terms of the algebraic equation as
\[\Rightarrow 4x+2y=300\]
Now, the algebraic representation of the given system is
\[\begin{align}
& 2x+y=160 \\
& 4x+2y=300 \\
\end{align}\]
Now, let us write the above both equations in terms of y
\[\Rightarrow y=160-2x\]
\[\Rightarrow y=\dfrac{300-4x}{2}\]
Now, let us find few corresponding values to represent them geometrically
| x | 50 | 60 | 70 |
| y | 60 | 40 | 20 |
| x | 40 | 50 | 60 |
| y | 70 | 50 | 30 |
Now, plot these points to represent the situation geometrically

Here, we can observe that both the lines do not intersect each other and are parallel so they do not have a common solution which means they have no unique solution.
This shows the prices are different
Note:
Instead of finding the equations in terms of y to represent them geometrically, we can also express them in terms of x and they further consider the values respectively and then represent which also gives the same representation.
It is important to note that the two lines are parallel which means they have a trivial solution and no unique solution. It is also to be noted that while writing the equations we should not neglect any of the terms which change the corresponding equation.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




