
The correct order of ‘${\text{S}} - {\text{O}}$’ bond length is-
(A) ${\text{SO}}_3^{2 - } > {\text{SO}}_4^{2 - } > {\text{S}}{{\text{O}}_3} > {\text{S}}{{\text{O}}_2}$
(B) ${\text{SO}}_3^{2 - } > {\text{SO}}_4^{2 - } > {\text{S}}{{\text{O}}_2} > {\text{S}}{{\text{O}}_3}$
(C) ${\text{SO}}_4^{2 - } > {\text{SO}}_3^{2 - } > {\text{S}}{{\text{O}}_2} > {\text{S}}{{\text{O}}_3}$
(D) ${\text{SO}}_4^{2 - } > {\text{SO}}_3^{2 - } > {\text{S}}{{\text{O}}_3} > {\text{S}}{{\text{O}}_2}$
Answer
566.7k+ views
Hint: The average distance between the nuclei of the two bonded atoms is known as bond length.The number of covalent bonds in any molecule is known as its bond order. The bond length is inversely proportional to the bond order.
Formulae used:
${\text{Bond order}} = \dfrac{{{\text{Total number of bonds between two atoms}}}}{{{\text{Total number of canonical form}}}}$
\[{\text{Bond length}} \propto \dfrac{1}{{{\text{Bond order}}}}\]
Complete step by step solution:
We are given four species ${\text{SO}}_3^{2 - }$, ${\text{SO}}_4^{2 - }$, ${\text{S}}{{\text{O}}_3}$ and ${\text{S}}{{\text{O}}_2}$.
Determine the bond order of ${\text{SO}}_3^{2 - }$ as follows:
The structure of ${\text{SO}}_3^{2 - }$ is as follows:
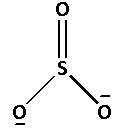
The number of bonds between the atoms in ${\text{SO}}_3^{2 - }$ is 4. The number of canonical forms of ${\text{SO}}_3^{2 - }$ is 3. The bond order of ${\text{SO}}_3^{2 - }$ is,
${\text{Bond order of SO}}_3^{2 - } = \dfrac{{\text{4}}}{{\text{3}}} = 1.33$
Thus, the bond order of ${\text{SO}}_3^{2 - }$ is 1.33.
Determine the bond order of ${\text{SO}}_4^{2 - }$ as follows:
The structure of ${\text{SO}}_4^{2 - }$ is as follows:
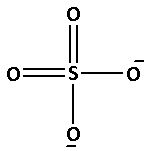
The number of bonds between the atoms in ${\text{SO}}_4^{2 - }$ is 6. The number of canonical forms of ${\text{SO}}_4^{2 - }$ is 4. The bond order of ${\text{SO}}_4^{2 - }$ is,
${\text{Bond order of SO}}_4^{2 - } = \dfrac{{\text{6}}}{{\text{4}}} = 1.5$
Thus, the bond order of ${\text{SO}}_4^{2 - }$ is 1.5.
Determine the bond order of ${\text{S}}{{\text{O}}_3}$ as follows:
The structure of ${\text{S}}{{\text{O}}_3}$ is as follows:
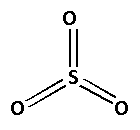
The number of bonds between the atoms in ${\text{S}}{{\text{O}}_3}$ is 6. The number of canonical forms of ${\text{S}}{{\text{O}}_3}$ is 3. The bond order of ${\text{S}}{{\text{O}}_3}$ is,
${\text{Bond order of S}}{{\text{O}}_3} = \dfrac{{\text{6}}}{{\text{3}}} = 2$
Thus, the bond order of ${\text{S}}{{\text{O}}_3}$ is 2.
Determine the bond order of ${\text{S}}{{\text{O}}_2}$ as follows:
The structure of ${\text{S}}{{\text{O}}_2}$ is as follows:
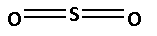
The number of bonds between the atoms in ${\text{S}}{{\text{O}}_2}$ is 6. The number of canonical forms of ${\text{S}}{{\text{O}}_2}$ is 3. The bond order of ${\text{S}}{{\text{O}}_2}$ is,
${\text{Bond order of S}}{{\text{O}}_2} = \dfrac{{\text{4}}}{{\text{2}}} = 2$
Thus, the bond order of ${\text{S}}{{\text{O}}_2}$ is 2.
Thus, the decreasing order of bond order is,
${\text{S}}{{\text{O}}_3} = {\text{S}}{{\text{O}}_2} > {\text{SO}}_4^{2 - } > {\text{SO}}_3^{2 - }$
The bond orders of ${\text{S}}{{\text{O}}_3}$ and ${\text{S}}{{\text{O}}_2}$ are same. But the bond pair-bond pair repulsion is higher in ${\text{S}}{{\text{O}}_3}$ and thus, the ${\text{S}} - {\text{O}}$ bond length in ${\text{S}}{{\text{O}}_3}$ is smaller than that in ${\text{S}}{{\text{O}}_2}$.
The bond length is inversely proportional to the bond order. Thus, the decreasing order of bond length is,
${\text{SO}}_3^{2 - } > {\text{SO}}_4^{2 - } > {\text{S}}{{\text{O}}_2} > {\text{S}}{{\text{O}}_3}$
Thus, the correct option is (B) ${\text{SO}}_3^{2 - } > {\text{SO}}_4^{2 - } > {\text{S}}{{\text{O}}_2} > {\text{S}}{{\text{O}}_3}$.
Note: The bond orders of ${\text{S}}{{\text{O}}_3}$ and ${\text{S}}{{\text{O}}_2}$ are same. But the bond pair-bond pair repulsion is higher in ${\text{S}}{{\text{O}}_3}$ and thus, the ${\text{S}} - {\text{O}}$ bond length in ${\text{S}}{{\text{O}}_3}$ is smaller than that in ${\text{S}}{{\text{O}}_2}$.
Formulae used:
${\text{Bond order}} = \dfrac{{{\text{Total number of bonds between two atoms}}}}{{{\text{Total number of canonical form}}}}$
\[{\text{Bond length}} \propto \dfrac{1}{{{\text{Bond order}}}}\]
Complete step by step solution:
We are given four species ${\text{SO}}_3^{2 - }$, ${\text{SO}}_4^{2 - }$, ${\text{S}}{{\text{O}}_3}$ and ${\text{S}}{{\text{O}}_2}$.
Determine the bond order of ${\text{SO}}_3^{2 - }$ as follows:
The structure of ${\text{SO}}_3^{2 - }$ is as follows:

The number of bonds between the atoms in ${\text{SO}}_3^{2 - }$ is 4. The number of canonical forms of ${\text{SO}}_3^{2 - }$ is 3. The bond order of ${\text{SO}}_3^{2 - }$ is,
${\text{Bond order of SO}}_3^{2 - } = \dfrac{{\text{4}}}{{\text{3}}} = 1.33$
Thus, the bond order of ${\text{SO}}_3^{2 - }$ is 1.33.
Determine the bond order of ${\text{SO}}_4^{2 - }$ as follows:
The structure of ${\text{SO}}_4^{2 - }$ is as follows:

The number of bonds between the atoms in ${\text{SO}}_4^{2 - }$ is 6. The number of canonical forms of ${\text{SO}}_4^{2 - }$ is 4. The bond order of ${\text{SO}}_4^{2 - }$ is,
${\text{Bond order of SO}}_4^{2 - } = \dfrac{{\text{6}}}{{\text{4}}} = 1.5$
Thus, the bond order of ${\text{SO}}_4^{2 - }$ is 1.5.
Determine the bond order of ${\text{S}}{{\text{O}}_3}$ as follows:
The structure of ${\text{S}}{{\text{O}}_3}$ is as follows:

The number of bonds between the atoms in ${\text{S}}{{\text{O}}_3}$ is 6. The number of canonical forms of ${\text{S}}{{\text{O}}_3}$ is 3. The bond order of ${\text{S}}{{\text{O}}_3}$ is,
${\text{Bond order of S}}{{\text{O}}_3} = \dfrac{{\text{6}}}{{\text{3}}} = 2$
Thus, the bond order of ${\text{S}}{{\text{O}}_3}$ is 2.
Determine the bond order of ${\text{S}}{{\text{O}}_2}$ as follows:
The structure of ${\text{S}}{{\text{O}}_2}$ is as follows:
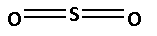
The number of bonds between the atoms in ${\text{S}}{{\text{O}}_2}$ is 6. The number of canonical forms of ${\text{S}}{{\text{O}}_2}$ is 3. The bond order of ${\text{S}}{{\text{O}}_2}$ is,
${\text{Bond order of S}}{{\text{O}}_2} = \dfrac{{\text{4}}}{{\text{2}}} = 2$
Thus, the bond order of ${\text{S}}{{\text{O}}_2}$ is 2.
Thus, the decreasing order of bond order is,
${\text{S}}{{\text{O}}_3} = {\text{S}}{{\text{O}}_2} > {\text{SO}}_4^{2 - } > {\text{SO}}_3^{2 - }$
The bond orders of ${\text{S}}{{\text{O}}_3}$ and ${\text{S}}{{\text{O}}_2}$ are same. But the bond pair-bond pair repulsion is higher in ${\text{S}}{{\text{O}}_3}$ and thus, the ${\text{S}} - {\text{O}}$ bond length in ${\text{S}}{{\text{O}}_3}$ is smaller than that in ${\text{S}}{{\text{O}}_2}$.
The bond length is inversely proportional to the bond order. Thus, the decreasing order of bond length is,
${\text{SO}}_3^{2 - } > {\text{SO}}_4^{2 - } > {\text{S}}{{\text{O}}_2} > {\text{S}}{{\text{O}}_3}$
Thus, the correct option is (B) ${\text{SO}}_3^{2 - } > {\text{SO}}_4^{2 - } > {\text{S}}{{\text{O}}_2} > {\text{S}}{{\text{O}}_3}$.
Note: The bond orders of ${\text{S}}{{\text{O}}_3}$ and ${\text{S}}{{\text{O}}_2}$ are same. But the bond pair-bond pair repulsion is higher in ${\text{S}}{{\text{O}}_3}$ and thus, the ${\text{S}} - {\text{O}}$ bond length in ${\text{S}}{{\text{O}}_3}$ is smaller than that in ${\text{S}}{{\text{O}}_2}$.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




