Question

The correct assumption made to perform a venturimeter experiment is (are).
A) that Bernoulli’s theorem holds good
B) that equation of continuity Is maintained
C) that the fluid used is highly incompressible
D) that all of the above are true

Answer 1

Hint:The venturimeter is the device which uses two measures the rate of flow of illiquid through a pipe. Basically it is an application of Bernoulli’s principle for an incomprehensible fluid.

Step by step solution:
The venturimeter is a device based on Bernoulli’s theorem for incompressible liquid.
We know the liquid which enters at one end must leave at the other end of the pipe. So it is also important to maintain the equation of continuity in the venturimeter.
 We know Bernoulli's theorem and equation of continuity both hold good for incompressible fluid.
It means in our question the option A, B and C all are correct its means in this question the option D is correct.
You understood more about venturimeter see the additional information.

Additional information:
Two understood the venturi meter we have to understand the working of venturimeter and its construction
It consists of a horizontal tube having a wide opening cross section ${A_1}$ and a narrow neck of cross section ${A_2}$ these two regions of the horizontal tube are connected to a manometer as shown in figure.

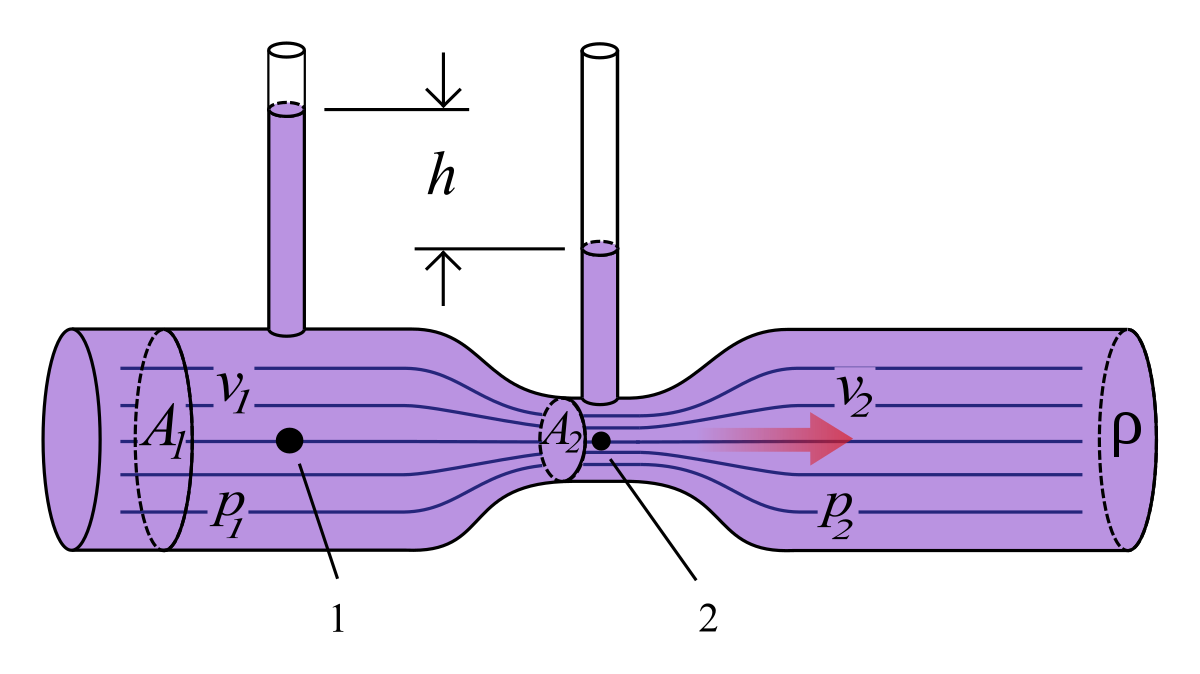
Let ${A_1}$ and ${A_2}$ be the areas of cross section of the tube and ${v_1}$ and ${v_2}$ is the velocities of flow of fluid and ${P_1}$ ${P_2}$ is the pressure at that point.
If we assume that the flow of water in the tube is streamlined.
If $\rho $ is the density of fluid and the flow of fluid in is horizontal then by Bernoulli’s theorem for the same horizontal level.
$
   \Rightarrow {P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \dfrac{1}{2}\rho {v_2}^2 \\
   \Rightarrow {P_1} - {P_2} = \dfrac{1}{2}\rho \left( {{v_2}^2 - {v_1}^2} \right) \\
 $
If $h$ be the difference in levels of fluid in the vertical tubes then.
$ \Rightarrow {P_1} - {P_2} = \rho gh$
Equate both equations.
$ \Rightarrow \rho gh = \dfrac{1}{2}\rho \left( {{v_2}^2 - {v_1}^2} \right)$
$ \Rightarrow {v_2}^2 - {v_1}^2 = 2gh$ .......... (1)
The rate of flow of fluid is same at every cross sectional area in pipe because the fluid is incompressible
Equation of Continuity
$ \Rightarrow {A_1}{v_1} = {A_2}{v_2}$
$ \Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{v_2}}}{{{v_1}}}$ ....... (2)
From equation (1)
$ \Rightarrow {v_1}^2\left[ {\left( {\dfrac{{{v_2}^2}}{{{v_1}^2}}} \right) - 1} \right] = 2gh$
From equation (2)
$ \Rightarrow {v_1}^2\left[ {\dfrac{{{A_1}^2}}{{{A_2}^2}} - 1} \right] = 2gh$
$ \Rightarrow {v_1}^2 = {A_2}^2\dfrac{{2gh}}{{{A_1}^2 - {A_2}^2}}$
$ \Rightarrow {v_1} = {A_2}\sqrt {\dfrac{{2gh}}{{{A_1} - {A_2}}}} $
If $Q$ be the volume of water flowing per second in the tube.
$\therefore Q = {A_1}{v_1} = {A_1}{A_2}\sqrt {\dfrac{{2gh}}{{{A_1}^2 - {A_2}^2}}} $
From this equation rate of can be determined.

Note:Here in the whole expression we used the equation of continuity as well as Bernoulli’s theorem for highly incompressible fluid. With the help of a venturimeter we can find the volume of liquid which flows per second from tube or at any cross sectional area of tube. As well as we can find the velocity of fluid at any point inside the tube.