Question

The coordinates of the one end of a diameter of a circle are $\left( 4,-1 \right)$ and co-ordinates of the centre of the circle are $\left( 1,-3 \right)$, then find the coordinates of the other end of the diameter are:
(a) $\left( 2,5 \right)$,
(b) $\left( -2,-5 \right)$,
(c) $\left( 3,2 \right)$,
(d) $\left( -3,-2 \right)$.

Answer 1

Hint: We start solving the problem by drawing the given information and assuming the other end of the diameter of the circle. We then use the fact that the centre of the circle is the midpoint of any diameter in that circle. We then use the fact that the midpoint of the line segment joining points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ for all the three points and make necessary calculations to get the other end of diameter..

Complete step-by-step solution
According to the problem, we are given that the point $\left( 4,-1 \right)$ is one end of a diameter of the circle and the point $\left( 1,-3 \right)$ is the center of that circle. We need to find the other end of the diameter of that circle.
Let us draw the given information to get a better view.

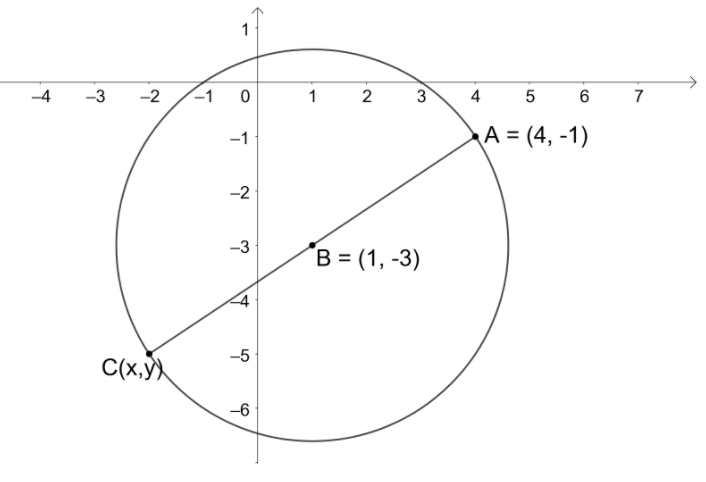
Let us assume the point $C\left( x,y \right)$ be the other end of the diameter of the given circle.
We know that the center of the circle is the mid-point of any diameter in that circle.
So, we get that the point $B\left( 1,-3 \right)$ is the midpoint of the line segment joining the points $A\left( 4,-1 \right)$ and $C\left( x,y \right)$.
We know that the midpoint of the line segment joining points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.
So, we get $\left( 1,-3 \right)=\left( \dfrac{4+x}{2},\dfrac{-1+y}{2} \right)$.
$\Rightarrow \dfrac{4+x}{2}=1$ and $\dfrac{-1+y}{2}=-3$.
$\Rightarrow 4+x=2$ and $-1+y=-6$.
$\Rightarrow x=-2$ and $y=-5$.
So, we get the coordinates of the point C as $\left( -2,-5 \right)$.
$\therefore$ The other end of the diameter of the circle is $\left( -2,-5 \right)$. The correct option for the given problem is (b).

Note: We can also solve this problem by finding the equation of circle and equation of diameter of the circle passing through the point $\left( 4,-1 \right)$. We then find the intersection of this diameter with the equation of the circle to get the other endpoint of diameter. Similarly, we can find the radius, area, and circumference of the circle using points. Similarly, we can expect problems to find the equation of tangents at both ends of the diameter.