Question

The coordinates of the midpoints of the sides of a triangle are (4,2), (3,3) and(2,2). What will be the coordinates of the centroid of the triangle?
A. $ \left( {3,\dfrac{7}{3}} \right) $
B. $ \left( { - 3, - \dfrac{7}{3}} \right) $
C. $ \left( {3, - \dfrac{7}{3}} \right) $
D. $ \left( { - 3,\dfrac{7}{3}} \right) $

Answer 1

Hint: To answer this type of problem we need to find the coordinates of the vertices of the triangle such that we can use the formula of the centroid and can calculate the coordinate of the centroid. In this problem coordinates of the mid points of the triangle are given so we will apply first the midpoint formula and find the sum of the coordinates for each side and in the last add all the three cases such that we will get the required coordinate of centroid.

Complete step-by-step answer:
Here suppose the triangle is given as in the diagram

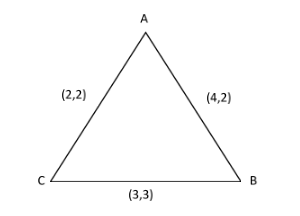
Suppose the coordinate of the vertices are A $ ({x_1},{y_1}) $ , B $ ({x_2},{y_2}) $ and C $ ({x_3},{y_3}) $
Coordinates of the midpoint of A and B are
\[
\Rightarrow {\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)} \\
\Rightarrow {\dfrac{{{x_1} + {x_2}}}{2} = 4,\dfrac{{{y_1} + {y_2}}}{2} = 2}
\]
\[{x_1} + {x_2} = 8\], \[{y_1} + {y_2} = 4\] ……….(1)
Similarly coordinates of mid-point of B and C are
\[\left( {\dfrac{{{x_2} + {x_3}}}{2},\dfrac{{{y_2} + {y_3}}}{2}} \right)\]
Or
\[\left( {\dfrac{{{x_2} + {x_3}}}{2} = 3,\dfrac{{{y_2} + {y_3}}}{2} = 3} \right)\]
Or
\[{x_2} + {x_3} = 6,{y_2} + {y_3} = 6\] ……………….(2)

Similarly coordinates of midpoint of C and A are
\[\left( {\dfrac{{{x_{1}} + {x_3}}}{2},\dfrac{{{y_{1}} + {y_3}}}{2}} \right)\]
Or
\[\left( {\dfrac{{{x_{1}} + {x_3}}}{2} = 2,\dfrac{{{y_{1}} + {y_3}}}{2} = 2} \right)\]
Or
\[{x_ 1} + {x_ 3} = 4,{y_1} + {y_3} = 4\] …………(3)
We know that the coordinate of centroid of a triangle is \[\left( {\dfrac{{{x_{1}} + {x_2} + {x_3}}}{3},\dfrac{{{y_{1}} + {y_2} + {y_3}}}{3}} \right)\]
So to find these coordinate just add all the equations means add equation (1), (2) and (3)
We get
\[
\Rightarrow 2\left({x_1} + {x_2} + {x_3} \right) = 18,2\left({y_1} + {y_2} + {y_3} \right) = 14 \\
\Rightarrow {x_1} + {x_2} + {x_3} = 9,{y_1} + {y_2} + {y_3} = 7 \\
\]
\[{x_1} + {x_2} + {x_3} = 9,{y_1} + {y_2} + {y_3} = 7\]………………(4)
No we know that centroid of a triangle is \[\left( {\dfrac{{{x_{1}} + {x_2} + {x_3}}}{3} = 3,\dfrac{{{y_{1}} + {y_2} + {y_3}}}{3} = \dfrac{7}{3}} \right)\] \[\left( {\dfrac{{{x_{1}} + {x_2} + {x_3}}}{3},\dfrac{{{y_{1}} + {y_2} + {y_3}}}{3}} \right)\]
So just divide the LHS and RHS of equation (4)
We get
\[\Rightarrow \dfrac{{{x_{1}} + {x_2} + {x_3}}}{3} = 3,\dfrac{{{y_{1}} + {y_2} + {y_3}}}{3} = \dfrac{7}{3}\]
So the centroid of triangle
\[\Rightarrow \left( {\dfrac{{{x_{1}} + {x_2} + {x_3}}}{3} = 3,\dfrac{{{y_{1}} + {y_2} + {y_3}}}{3} = \dfrac{7}{3}} \right)\]
Or centroid = $ \left( {3,\dfrac{7}{3}} \right) $
So, the correct answer is “Option A”.

Note: In this problem we can also find the coordinate of the centroid by firstly finding the coordinate of all vertices then finding the coordinate of the centroid. But that is quite lengthy than the above mentioned method.