Question

The coordinates of a uniform rod placed as shown are:

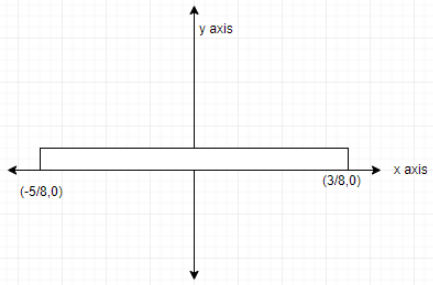
A: (0,0)
B: (1/8, 0)
C: (1/8,0)
D: (-1/2,0)

Answer 1

Hint:Centre of mass of any object can be defined as a unique point in space where the mass of the particle becomes equal to the mass of the object for the application of Newton’s laws of motion. Geometrically, we can find the coordinates of the centre of mass very easily.

Complete step by step answer:
Upon observation, we can understand that the points are distanced at a length of 1m from each other. Since it is a uniform rod that lies on the x axis, we can say that the value of the y coordinate will always be zero. The focus should be given to the x coordinates of the centre of mass.The centre of mass of the system is at a distance of $\dfrac{1}{2}$ units from (-5/8,0).
Hence, the x coordinate is
$-\dfrac{5}{8}+\dfrac{1}{2}=-\dfrac{1}{8}$
Hence we can arrive at a conclusion that the centre of mass of the system is located at the point $(-\dfrac{1}{8},0)$

Thus, option C is the correct answer among the four given options in the question.

Note:Here we are given a uniform rod. If it is a non-uniform rod, then the centre of mass can be calculated by forming an equation that shows its mass using a small element and integrating this element of mass to get the mass of the entire rod. Later we can find the centre of mass from mathematical equations. This point is to be noted by the students.