Question

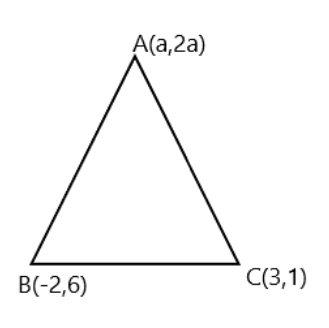
The coordinates of A for which area of triangle, whose vertices are $ A(a,2a),B( - 2,6) $ and $ C(3,1) $ is $ 10 $ square units are:

A. $ (0,3) $
B. $ (5,8) $
C. $ \left( {3,\dfrac{8}{3}} \right) $
D. None of these

Answer 1

Hint: As we know that the above question is related to the coordinate geometry. We know the formula of area of triangle is $ \dfrac{1}{2}\left[ {{a_1}({b_1} - {b_2}) + {b_1}({c_1} - {c_2}) + {c_1}({a_1} - {a_2})} \right] $ , where $ \left[ {({b_1} - {b_2}),({c_1} - {c_2})and({a_1} - {a_2})} \right] $ are the coordinates of vertices of triangle. We will apply this formula of area of the triangle and find the value of $ a $ .

Complete step by step solution:
Here in this question, the area is $ 10 $ square units. We have
 $ {a_1} = a,{a_2} = 2a,{b_1} = - 2,{b_2} = 6 $ and $ {c_1} = 3 $ , $ {c_2} = 1 $ .
Are of triangle is
 $ \dfrac{1}{2}\left[ {{a_1}({b_1} - {b_2}) + {b_1}({c_1} - {c_2}) + {c_1}({a_1} - {a_2})} \right] $ , by putting the values we have:
$ 10 = \dfrac{1}{2}\left[ {a\left( {-2 - 6} \right) + ( - 2)\left( {3 - 1} \right) + 3\left( {a - 2a} \right)} \right] $ .
We will now solve it,
$ -8a - 4 - 3a = 20 \\
\Rightarrow -11a = 24
 $
On further solving we have $ a = -\dfrac{{24}}{{11}} $ and then $ 2a = 2 \times -\dfrac{24}{11} = -\dfrac{{48}}{11} $ .
Hence the correct option is (D).
So, the correct answer is “Option D”.

Note: Before solving this kind of question we should have the proper knowledge of triangles, their area and the vertices. Sometimes we get a quadratic equation while finding the value of required missing number, then we can find the value of roots by the method of quadratic formula i.e. $ \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ .