Question

The coordinates for a rhombus are given as $(2a,0),(0,2b),( - 2a,0),and(0, - 2b)$ . How does one prove that the midpoints of the sides of a rhombus determine a rectangle using coordinate geometry?

Answer 1

Hint: The Midpoint Formula works precisely the same way as If you would like to search out the purpose that's exactly halfway between two given points, just average the x-values and therefore the y-values.

Complete step-by-step solution:
Let the coordinates of a rhombus as
$A(2a,0),B(0,2b),C( - 2a,0)$ and $D(0, - 2b)$ .
Let the midpoint of $AB$be $P$ .
Therefore , coordinates are given as ,
$P = \left( {\dfrac{{0 + 2a}}{2},\dfrac{{0 + 2b}}{2}} \right) = (a,b)$
Let the midpoint of $BC$be $Q$ .
Therefore , coordinates are given as ,
$Q = \left( {\dfrac{{ - 2a + 0}}{2},\dfrac{{0 + 2b}}{2}} \right) = ( - a,b)$
Let the midpoint of $CD$be $R$ .
Therefore , coordinates are given as ,
$R = \left( {\dfrac{{0 - 2a}}{2},\dfrac{{ - 2b + 0}}{2}} \right) = ( - a, - b)$
Let the midpoint of $DA$be $S$ .
Therefore , coordinates are given as ,
$S = \left( {\dfrac{{2a + 0}}{2},\dfrac{{0 - 2b}}{2}} \right) = (a, - b)$
It can be seen that $P$ lies in quadrant $I$, $Q$ in Quadrant $II$ , $R$ in $III$ and $S$ in $IV$, Further $P$ and $Q$ are the reflections of each other in y-axis, $Q$ and $R$ are the reflections of each other in x-axis, $R$ and $S$ are reflection of each other in y -axis and $S$ and $P$ are reflection of each other in x -axis.

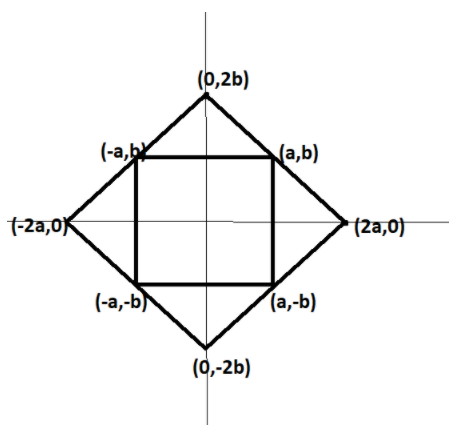
Hence, the mid points of the rhombus form the rectangle.

Note: Sometimes you would like to seek out the purpose that's exactly midway between two other points. For example, you may find a line that bisects (divides into two equal halves) a given line segment. This middle point is named the "midpoint". The concept doesn't come up often, but the Formula is sort of simple and obvious, so you must easily be able to recall it for later.