Question

The coordinates (12, 8), (-2, 6), (6, 0) form a right angle triangle and find the area of the triangle.

Answer 1

Hint – In order to solve this problem apply the distance formula to get the lengths of sides of the triangle and then observe which can be the height and base of the triangle using Pythagoras theorem and then find the area of the right angle triangle using the respective formula.

Complete step-by-step solution -
 The triangle can be shown in figure as:

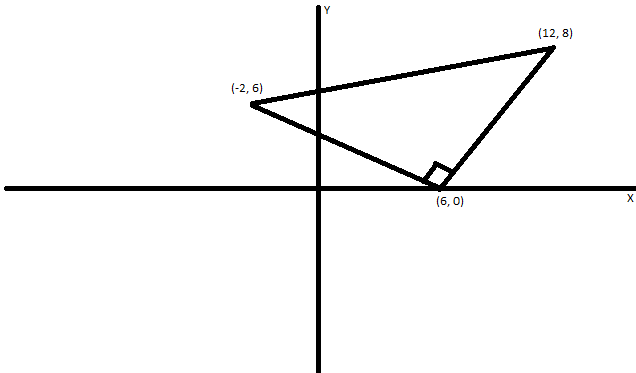
We know that the distance between the point (a, b) and (c, d) can be written as,
$ \Rightarrow \sqrt {{{(a - c)}^2} + {{(b - d)}^2}} $.
So, the distance between the points (12, 8) and (-2, 6) can be obtained as,
$\begin{gathered}
   \Rightarrow \sqrt {{{(12 - ( - 2))}^2} + {{(8 - 6)}^2}} \\
   \Rightarrow \sqrt {{{14}^2} + {2^2}} = \sqrt {196 + 4} = \sqrt {200} = 10\sqrt 2 \\
\end{gathered} $
And the distance between the points (12, 8) and (6, 0) can be written as,
$
   \Rightarrow \sqrt {{{(12 - 6)}^2} + {{(8 - 0)}^2}} \\
   \Rightarrow \sqrt {{6^2} + {8^2}} = \sqrt {36 + 64} = \sqrt {100} = 10 \\
$
Similarly, we will find the distance between (6, 0) and (-2, 6) as,
$
   \Rightarrow \sqrt {{{(6 - ( - 2))}^2} + {{(0 - 6)}^2}} \\
   \Rightarrow \sqrt {{8^2} + {6^2}} = \sqrt {64 + 36} = \sqrt {100} = 10 \\
$
We can clearly see that the longest side with length $10\sqrt 2 $ is the hypotenuse whereas the lengths of height and base are 10 units both.
As we know that the area of the right-angled triangle is $\dfrac{{\text{1}}}{{\text{2}}}{\text{(base)(height)}}$
On putting the value of base and height as 10 units. Then we got the area as,
${\text{Area = }}\dfrac{{\text{1}}}{{\text{2}}}{\text{(10)(10) = }}\dfrac{{{\text{100}}}}{{\text{2}}}{\text{ = 50}}\,{\text{unit}}{{\text{s}}^{\text{2}}}$
Hence the answer to this problem is 50.

Note – To solve this problem we just need to know the lengths of base and height and then calculate the area by using the formula that area is equal to $\dfrac{{\text{1}}}{{\text{2}}}{\text{(base)(height)}}$. Here we have used the distance formula as well to calculate the lengths of sides of the triangle. Proceeding like this you can solve your problem.Another approach to solve this problem is heron’s formula where, first we had to find the half perimeter of triangle(s) and then the heron’s formula in terms of s and length of the sides of triangle.