Question

The construction of $\vartriangle LMN$ in which LM = 8 cm, $\angle L = {45^ \circ }$ is possible when (MN + LN) is
A) 6 cm
B) 7 cm
C) 9 cm
D) 5 cm

Answer 1

Hint: We will use the fact that the sum of length of the two sides of a triangle is always, no matter what is greater than the length of the third side. Seeing this fact, we will be left with two one options only.

Complete step-by-step answer:
We will first learn about the triangle inequality.
The triangle inequality rule states that the length of a side of a triangle is less than the sum of the lengths of the other two sides and greater than the difference of the lengths of the other two sides.
Now, we have the triangle:

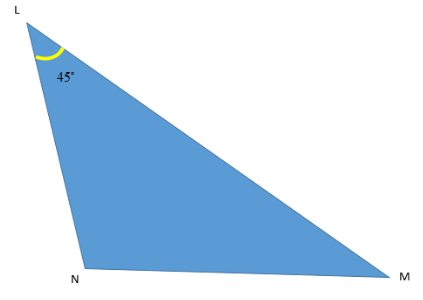
So on using the triangle inequality mentioned above, we will get:
$ \Rightarrow $MN + LN > LM
And since LM is given to be 8 cm long.
So, let us put this in the above formula. Then, we will get:
$ \Rightarrow $So, MN + LN > 8.
Now, looking at the options, we see that only one of the options is possible to be the answer.
Hence, MN + LN can be 9 cm.
Because all the options other than 9 cm are 7 cm, 6 cm and 5 cm which are less than 8 cm.

Hence, the correct option is (C).

Note: The students might get confused on seeing the angle given in the data in question, which actually has no use in the solution as such.
The students must notice that the property they used, that is the inequality can be proved as well.
Here is the proof of it:
Consider we have $\vartriangle ABC$ already with us. Construct the line AB in such a way that after its extension: AC = AD.

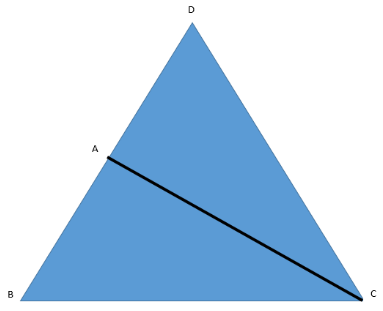
Now, we know that angles opposite to equal sides are equal in a triangle. Therefore, in $\vartriangle ACD$:
Since AC = AD, we will get:- $\angle ADC = \angle ACD$.
Therefore, if we add anything positive to any one side, that side will increase.
Therefore, $\angle ADC + \angle BCA > \angle ACD$
On simplifying the LHS, we will get:-
$ \Rightarrow $$\angle C > \angle ACD$
Since, the sides opposite to greater angle is greater in size in a triangle. Therefore, in $\vartriangle ABC$ we have: BD > BC.
We can write it as:-
$ \Rightarrow $AB + AD > BC
Rewriting again by making modification, we will get:-
$ \Rightarrow $AB + AC > BC
Hence, proved.
We can prove the same over any side using the same technique.