Question

The common tangents to ${x^2} + {y^2} - 10y = 0$ and ${x^2} + {y^2} + 6y = 0$ form a triangle . Then the correct option is
a.Triangle is isosceles but not equilateral
b.Triangle is equilateral
c.Area of the triangle is ${\left( {15} \right)^{\dfrac{3}{2}}}$ sq. units
d.Area of the triangle is 15 sq. units

Answer 1

Hint: We know that the general equation of a circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$ whose centre and radius is given by $\left( { - g, - f} \right){\text{ and }}\sqrt {{g^2} + {f^2} - c} $.using this we can find the centre and radius of the two circles and by finding the distance between the two centres using the formula$\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $ we get that it is equal to the sum of the radii of the circles .Hence the circles touch each other externally and by using the property that the length of tangents from an external point to a circle are equal. we can show that the triangle formed is a isosceles triangle

Complete step-by-step answer:
We are given equations of two circles ${x^2} + {y^2} - 10y = 0$and ${x^2} + {y^2} + 6y = 0$
We know that the general equation of a circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$
Its centre and radius is given by $\left( { - g, - f} \right){\text{ and }}\sqrt {{g^2} + {f^2} - c} $
Let's consider the circle ${x^2} + {y^2} - 10y = 0$
Here $2g = 0{\text{ and }}2f = - 10$
Hence $g = 0{\text{ and }}f = - 5$
Therefore its centre is $\left( { - g, - f} \right) = \left( {0,5} \right)$
And radius is $\sqrt {{0^2} + {{\left( { - 5} \right)}^2} - 0} = \sqrt {25} = 5units$
 Let's consider the circle ${x^2} + {y^2} + 6y = 0$
Here $2g = 0{\text{ and }}2f = 6$
Hence $g = 0{\text{ and }}f = 3$
Therefore its centre is $\left( { - g, - f} \right) = \left( {0, - 3} \right)$
And radius is $\sqrt {{0^2} + {{\left( 3 \right)}^2} - 0} = \sqrt 9 = 3units$
Let's find the distance between the centres
$
   \Rightarrow \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( {0 - 0} \right)}^2} + {{\left( {5 - ( - 3)} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 8 \right)}^2}} = 8units \\
$

Sum of radii = 5 + 3 =8 units
Therefore the distance between the centres is equal to the sum of their radii
Hence the circles touch each other externally

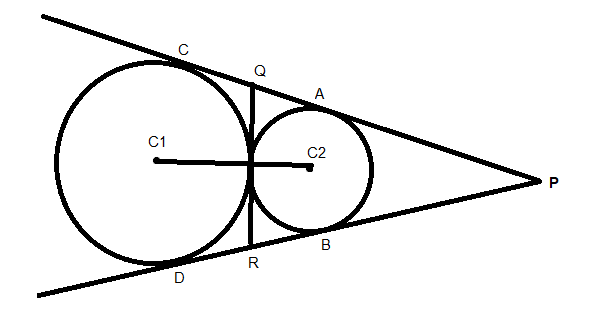
Now the tangents touch the circle ${x^2} + {y^2} - 10y = 0$at C and D and touch the circle ${x^2} + {y^2} + 6y = 0$ at A and B
Let PQR be the triangle formed
By the property ,
The length of tangents from an external point to a circle are equal.
$ \Rightarrow PA = PB$……..(1)
$ \Rightarrow PC = PD$ …….(2)
From this
We get that $AC = BD$ ……..(3)
And $AQ = BR$ ……..(4)
Adding (1) and (4) we get
$
   \Rightarrow PA + AQ = PB + BR \\
   \Rightarrow PQ = PR \\
$
Therefore we get that the two sides of the triangle PQR are equal .
Hence it is an isosceles triangle
The correct option is a.

Note: The tangent always touches the circle at a single point.
It is perpendicular to the radius of the circle at the point of tangency
It never intersects the circle at two points.