Question

The combined equation of the two sides of an equilateral triangle is ${{x}^{2}}-3{{y}^{2}}-2x+1=0$. If the length of a side of the triangle is \[4\] then the equation of the third side is
(a)$x=2\sqrt{3}+1$
(b)$y=2\sqrt{3}+1$
(c)$x+2\sqrt{3}=1$
(d)$x=-2\sqrt{3}+1$

Answer 1

Hint: First find out the two sides equation from the given equation. Then find out the point of intersection of these two sides. Then proceed with finding the third side equation from the obtained values.

Complete step-by-step answer:
 Two sides of an equilateral triangle are represented by ${{x}^{2}}-3{{y}^{2}}-2x+1=0$.
By rearranging the terms, we get
\[{{x}^{2}}-2x+1=3{{y}^{2}}\]
The LHS is a quadratic equation, and we know $\left[ {{a}^{2}}-2ab+{{b}^{2}}={{(a-b)}^{2}} \right]$, so we can write the given equation as,
\[{{(x-1)}^{2}}=3{{y}^{2}}\]
Taking square root on both sides, we get
\[\begin{align}
  & (x-1)=\pm \sqrt{3{{y}^{2}}} \\
 & \Rightarrow x-1=\pm \sqrt{3}y \\
\end{align}\]
This can be split into two equations as follows,
\[x+\sqrt{3}y-1=0,x-\sqrt{3}y-1=0\]
So, these are the two sides of the equilateral triangle represented by ${{x}^{2}}-3{{y}^{2}}-2x+1=0$.
Now we will find the intersection point of these two sides.
Adding the above two equations, we get
\[\begin{align}
  & x+\sqrt{3}y-1+x-\sqrt{3}y-1=0 \\
 & \Rightarrow 2x-2=0 \\
 & \Rightarrow 2x=2 \\
 & \Rightarrow x=1 \\
\end{align}\]
Putting the value of ‘x’ in any of the two equations, we get
\[\begin{align}
  & 1+\sqrt{3}y-1=0 \\
 & \Rightarrow \sqrt{3}y=0 \\
 & \Rightarrow y=0 \\
\end{align}\]
So, the two sides triangle intersect at point \[(1,0).\]
It is given that the third side is of length \[4\] units.
Let us represent these as diagrams as shown below.

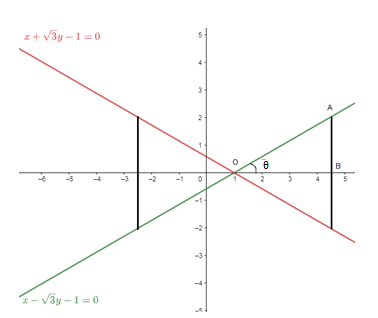
As the angle between the sides of triangle should be ${{60}^{\circ }}$ as it is equilateral triangle, so from the figure it is clear that the third side has two possibilities, i.e., the third side will be perpendicular to x-axis on either side of y-axis, i.e., they have equal and opposite x-intercept.
Now consider the line \[x-\sqrt{3}y-1=0\], this can be written as,
$\begin{align}
  & \sqrt{3}y=x-1 \\
 & \Rightarrow y=\dfrac{1}{\sqrt{3}}x-\dfrac{1}{\sqrt{3}} \\
\end{align}$
So, the slope of this line will be $\dfrac{1}{\sqrt{3}}$ .
We know angle between a line and x-axis is given by the formula,
\[\tan \theta =m=\dfrac{\Delta y}{\Delta x}\]
Here ‘m’ is the slope of the line.
Using this formula, we will find the angle between line \[x-\sqrt{3}y-1=0\] and x-axis, so we have
\[\tan \theta =\dfrac{1}{\sqrt{3}}=\dfrac{AB}{OB}\]
As the third side of the triangle if of length $4$and x-axis is dividing the third side into two equal parts, so
$AB=2$
Substituting this in the above equation, we get
\[\begin{align}
  & \tan \theta =\dfrac{1}{\sqrt{3}}=\dfrac{2}{OB} \\
 & \Rightarrow OB=2\sqrt{3} \\
\end{align}\]
As the point O is at a distance of $1$ unit from the origin, so the x-coordinate of the third line will be,
$\begin{align}
  & OB+1 \\
 & \Rightarrow 2\sqrt{3}+1 \\
\end{align}$
As the third equation is parallel to the y-axis, so the equation of the third line will be the x-coordinate.
Therefore, the two possible equations of the third side is,
$\begin{align}
  & x=\pm 2\sqrt{3}+1 \\
 & \Rightarrow x=2\sqrt{3}+1,x=-2\sqrt{3}+1 \\
\end{align}$
Hence the correct answer is option (a), (c), (d) .

Note: If the student does not make a diagram of the given question, there are chances he will miss the other equation of the third side.