Question

The coefficients of static friction and kinetic friction between the two blocks and also between the lower block and the ground are ${\mu _s} = 0.6$, and ${\mu _k} = 0.4$ . Find the value of tension $T$ applied on the lower block at which the upper block begins to slip relative to the lower block.

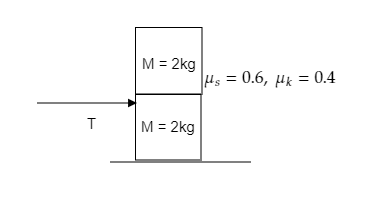
a. 20 N
b. 40 N
c. 60 N
d. 80 N

Answer 1

Hint: “T” is the force that must be applied on the lower block to get acceleration, i.e., for it to start moving. As it is in motion kinetic friction comes into light. The acquired acceleration provides the necessary force for the upper block to overcome its static friction and begin to slip.

Formula used:
- Maximum static friction (i.e., if the applied force exceeds this limiting value of static friction the body starts to slide on the surface), ${({f_s})_{\max }} = {\mu _s}N = {\mu _s}mg$ where ${({f_s})_{\max }}$ is the maximum static friction, $N = mg$is the normal force ( $m$ is the mass of the body and $g$ is the acceleration due to gravity), ${\mu _s}$ is the coefficient of static friction (depends on the nature of surfaces in contact)
- Kinetic friction $({f_k})$ which is the frictional force that opposes the relative motion between the surfaces in contact is given by, ${f_k} = {\mu _k}N = {\mu _k}mg$ , where ${\mu _k}$ is the coefficient of kinetic friction and $N = mg$ is the normal force ( $m$ is the mass of the body and $g$ is the acceleration due to gravity)
- Force $F$, acting on a body of mass $m$ to produce an acceleration of $a$ is given as $F = ma$

Complete step by step answer:
Step 1: List the information given in the question.
We have, the coefficient of static friction between the two blocks and that between the ground and the lower block as ${\mu _s} = 0.6$
Also, the coefficient of kinetic friction between the lower block and the ground $ = {\mu _k} = 0.4$
Masses of two blocks $ = {m_1} = {m_2} = 2{\text{kg}}$

Step 2: Express the relation for the maximum static friction, between the ground and the lower block and that between the two blocks

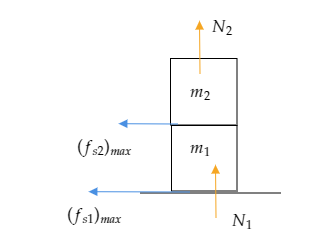
Maximum static friction between the ground and the lower block is given by, ${({f_{s1}})_{\max }} = {\mu _s}{N_1} = {\mu _S}({m_1} + {m_2})g$ , where ${\mu _s}$ represents the coefficient of static friction between the ground and lower block, ${m_1}$ and ${m_2}$ represent the masses of the lower and upper blocks respectively and $g = 10{\text{m/s}}$ is the acceleration due to gravity. Note that ${N_1} = ({m_1} + {m_2})g$ represents the normal force acting on the lower block.
Maximum static friction between the two blocks is given by, ${({f_{s2}})_{\max }} = {\mu _s}{N_2} = {\mu _S}{m_2}g$ where ${\mu _s}$ represents the coefficient of static friction between the two blocks, ${m_1}$ and ${m_2}$ represent the masses of the lower and upper blocks respectively and $g = 10{\text{m/s}}$ is the acceleration due to gravity. Note that ${N_2} = {m_2}g$ represents the normal force acting on the upper block.

Step 3: Calculate ${({f_{s1}})_{\max }}$ and ${({f_{s2}})_{\max }}$ by substituting values of ${\mu _s} = 0.6{\text{, }}{m_1} = {m_2} = 2{\text{kg}}$ and $g = 10{\text{m/s}}$
We have, ${({f_{s1}})_{\max }} = {\mu _S}({m_1} + {m_2})g$
Substituting the values, ${({f_{s1}})_{\max }} = 0.6 \times (2 + 2) \times 10 = 24{\text{N}}$
So, we must apply a tension $T > 24{\text{N}}$ to get the lower block moving along the ground.
We have, ${({f_{s2}})_{\max }} = {\mu _S}{m_2}g$
Substituting the values, ${({f_{s2}})_{\max }} = 0.6 \times 2 \times 10 = 12{\text{N}}$
Hence, there exists static friction ${({f_{s2}})_{\max }} = 12{\text{N}}$ when the upper block begins to slip.
Once the lower block starts moving the kinetic friction ${f_k}$ comes in to play.

Step 4: Express the relation for the kinetic friction, ${f_k}$acting on the system

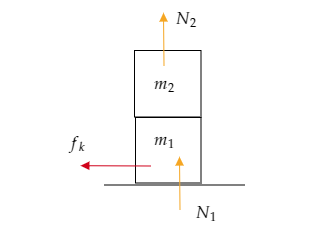
Kinetic friction acting on the lower block is given by, ${f_k} = {\mu _k}{N_1} = {\mu _k}({m_1} + {m_2})g$ , where ${\mu _k}$ represents the coefficient of kinetic friction between the ground and the lower block, ${m_1}$ and ${m_2}$ represent the masses of the lower and upper blocks respectively and $g = 10{\text{m/s}}$ is the acceleration due to gravity.
Note that ${N_1} = ({m_1} + {m_2})g$ represents the normal force acting on the lower block.
Step 5: Calculate ${f_k}$ by substituting values of ${\mu _k} = 0.4{\text{, }}{m_1} = {m_2} = 2{\text{kg}}$ and $g = 10{\text{m/s}}$
We have, ${f_k} = {\mu _k}({m_1} + {m_2})g$
Substituting the values, ${f_K} = 0.4 \times (2 + 2) \times 10 = 16{\text{N}}$
Therefore, once the block starts moving along the ground a force of ${f_K} = 16{\text{N}}$ opposes it.

Step 6: Express the equation for the net force acting on the lower block as it moves
The forces in play as the block moves along the ground are
Tension $T$ applied to the lower block
Kinetic friction ${f_K} = 16{\text{N}}$ that opposes its motion
Then, the net force $F = T - {f_k}$
We know $F = ma = ({m_1} + {m_2})a$ as the total mass of the system is $m = {m_1} + {m_2}$
Now the force equation becomes, $F = ({m_1} + {m_2})a = T - {f_k}$

Step 7: Obtain the equation for the acceleration $a$ of the system
Net force $F = ({m_1} + {m_2})a = T - {f_k}$
Rearranging we get, $a = \dfrac{{T - {f_k}}}{{({m_1} + {m_2})}}$
Substituting values of ${f_K} = 16{\text{N, }}{m_1} = {m_2} = 2{\text{kg}}$ , we have $a = \dfrac{{T - 16}}{{(2 + 2)}} = \dfrac{{T - 16}}{4}$
Hence, when the relative motion begins, the acceleration of the system is $a = \dfrac{{T - 16}}{4}$

Step 8: Make use of the above relation for acceleration to find the tension $T$at which the upper block begins to slip relative to the lower block
The maximum static friction that exists between the two blocks once the lower block starts to move is ${({f_{s2}})_{\max }} = 12{\text{N}}$
When the upper block begins to slip its acceleration is $a = \dfrac{{T - 16}}{4}$
And, the corresponding force will be ${m_2}a = {m_2}\left( {\dfrac{{T - 16}}{4}} \right)$
Substituting ${m_2} = 2{\text{kg}}$ in the above equation, we get ${m_2}a = 2 \times \left( {\dfrac{{T - 16}}{4}} \right) = \dfrac{{T - 16}}{2}$
At the instance, the upper block slips the above force ${m_2}a$must be equal to the static friction between the two blocks.
So, ${m_2}a = \dfrac{{T - 16}}{2} = 12{\text{N}}$
Cross multiplying, we get $T = (12 \times 2) + 16$
On solving we get, $T = 40{\text{N}}$.
Therefore, a tension $T = 40{\text{N}}$ is applied on the lower block at which the upper block begins to slip relative to the lower block.

Hence, the correct answer is option (B).

Note: The normal forces ${N_1}$ and ${N_2}$ are balanced by the weight of the blocks. While writing the net force equation make sure all the forces that are acting on the body are considered. It is only when a body overcomes the static friction that it starts to move. And as it moves the kinetic friction will try to oppose its motion.