Question

The coefficient of viscosity of a liquid does not depend upon
(A) The density of liquid.
(B) Temperature of liquid.
(C) Pressure of liquid.
(D) Nature of the liquid

Answer 1

Hint : The viscosity of a fluid is expressed as the ratio of shear stress to shear rate of that fluid. Thus, we can say that it does not change with mass or volume of the liquid.

Formula Used: The following formulas are used to solve this question.
 $ \tau \alpha \dfrac{{d\theta }}{{dt}} $ where, shear stress is $ \tau $ and $ \dfrac{{d\theta }}{{dt}} $ is the rate of angular deformation.

Complete step by step answer
Viscosity is an important rheological measurement that deals with the resistance to flow. It is a physical property that explains this resistance.
Viscosity is defined as the degree up to which a fluid resists the flow under an applied force and it is measured by the tangential friction force acting per unit area divided by the velocity gradient under conditions of streamline flow.
 $ {\text{Viscosity = }}\dfrac{{{\text{shear stress}}}}{{{\text{shear rate}}}} $
The viscosity is calculated in terms of the coefficient of viscosity. The value of this coefficient constant for a liquid depends on its liquid’s nature. In case of liquids the reason of viscosity is molecular bonding, so when we increase the temperature of liquid these molecular bonds break due to which viscosity decreases. Whereas in case of gases the reason of viscosity is molecular collision, so when we increase the temperature of gas collision between molecules increases and hence the viscosity increases. In a similar fashion, pressure also affects the viscosity coefficient.
We know that, in case of fluids, shear stress $ \left( \tau \right) $ is directly proportional to rate of shear strain, also known as the rate of angular deformation. The rate of angular deformation is represented by $ \dfrac{{d\theta }}{{dt}} $ .
 $ \therefore \tau \alpha \dfrac{{d\theta }}{{dt}} $
 $ \Rightarrow \tau = \mu \dfrac{{d\theta }}{{dt}} $
Since, $ \dfrac{{d\theta }}{{dt}} = \dfrac{{du}}{{dy}} $ , as shown above, it can be written that,
 $ \tau = \mu \dfrac{{du}}{{dy}} $
Thus, the coefficient of viscosity is a function of shear stress and is independent of its density.
The correct answer is Option A.

Note
We can also derive the value of the shear stress by the following method. For a very small elemental thickness of fluid consisting only two layers of fluid, flowing one over another. Let the fluid is flowing with the velocity ' $ u $ ' and ' $ t $ ' represents time. Let ' $ dy $ ' be the small distance between two layers of fluid.

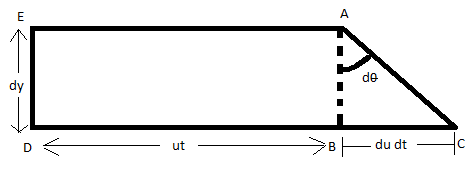
In the given figure, AB and BC represents differential distance.
 $ \therefore $ It is obvious from the figure that $ BC = dudt $ and the distance DB is the product of the speed and time and is given as $ ut $ .
In $ \Delta ABC $ ,
 $ \tan \left( {d\theta } \right) = \dfrac{{dudt}}{{dy}} $ , since $ \tan \theta = \dfrac{{perpendicular}}{{base}} $
 $ \Rightarrow d\theta = \dfrac{{dudt}}{{dy}} $ '
 $ \Rightarrow \dfrac{{d\theta }}{{dt}} = \dfrac{{du}}{{dy}} $ , where $ \dfrac{{d\theta }}{{dt}} $ represents the rate of deformation and $ \dfrac{{du}}{{dy}} $ represents the velocity gradient.
Now, shear stress $ \left( \tau \right) $ is directly proportional to shear strain, thus $ \tau \alpha \dfrac{{d\theta }}{{dt}} $ where $ \dfrac{{d\theta }}{{dt}} $ is the rate of angular deformation.
 $ \Rightarrow \tau = \mu \dfrac{{d\theta }}{{dt}} $ .
 Since, $ \dfrac{{d\theta }}{{dt}} = \dfrac{{du}}{{dy}} $ , as shown above, hence it is proved that,
 $ \tau = \mu \dfrac{{du}}{{dy}} $ .
The Poiseuille’s method is formally used to estimate the coefficient of viscosity, in which the liquid flows through a tube at the different level of pressures.