Question

The coefficient of friction $\mu $ is equal to.

$\begin{align}
  & A.0.10 \\
 & B.0.15 \\
 & C.0.20 \\
 & D.0.30 \\
\end{align}$

Answer 1

Hint: First of all consider the whole body as a system of mass in which the combined mass should be taken care. This will give an equation of force. Using this, write down the acceleration of the whole system which will give us another equation. By rearranging these equations in terms of acceleration and then comparing will give us the correct answer.

Complete step-by-step answer:
First of all let us draw the figure.

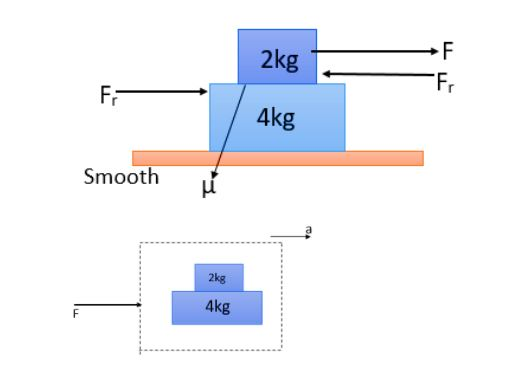
Until there is slipping between the masses, the whole system will be moving as one,
Therefore we can find the force acting on the system of masses by taking the combination of masses,
$F=\left( {{m}_{1}}+{{m}_{2}} \right)a$
Where
$\begin{align}
  & {{m}_{1}}=2kg \\
 & {{m}_{2}}=4kg \\
\end{align}$
Substituting the values in it will give,
$F=\left( 4+2 \right)a$
$F=6a$
From this we can find the frictional force acting on$2kg$,
That is, we can write that,
${{F}_{r}}=F-{{m}_{1}}a$
It is already given that,
$\begin{align}
  & {{m}_{1}}=2kg \\
 & {{m}_{2}}=4kg \\
 & F=0.5t \\
\end{align}$
And also consider the value of $t$at the time of slipping be
$t=12.5$

Substituting the values in the above obtained equations will give,
$F=\left( {{m}_{1}}+{{m}_{2}} \right)a$……….. (1)
${{F}_{r}}=F-{{m}_{1}}a$………….. (2)
Rearranging and comparing will leads to,
$a=\dfrac{0.5\times 12}{\left( 2+4 \right)}=1m{{s}^{-1}}$
From the equation (2), we can write that, after substituting the value of acceleration in it,
${{F}_{r}}=0.5\times 12-2\times 1=4$
Now the condition for slipping begins, which will give as the relation,
${{f}_{r}}\le {{f}_{r\max }}$
For simplifying or to find the answer, we can take the equality relation between them.
\[{{f}_{r}}={{f}_{r\max }}\]
That means we can write that,
\[4=\mu {{m}_{1}}g\]
Substituting the values in it,
\[4=\mu \times 2\times 10\]
Therefore after rearranging this equation, we will get the coefficient of friction,
That is,
\[\mu =0.2\]
Hence the coefficient of friction has been obtained.

So, the correct answer is “Option C”.

Note: Generally, the coefficient of kinetic friction is only dependent on the nature of the material of the surface. It is not dependent on any other factors. For example, the relative speed between the surfaces and the surface area in contact.