
The coach of a cricket team buys one bat and 2 balls for Rs.300. later he buys another 2 bats and 3 balls of the same kind for Rs.525. Represent this situation algebraically and solve it by graphical method. Also find out how much money the coach will pay for the purchase of one bat and one ball.
Answer
573.3k+ views
Hint: Assume the cost of one bat be x rupees and the cost of one ball be y rupees. Then we will formulate the given conditions into equations involving x and y and then solve the equations by elimination method and determining the value of x and y.
Complete step-by-step answer:
Let the cost of one bat be x rupees and the cost of one ball be y rupees.
In Algebraic form:
Then the equation for one bat and 2 balls costing Rs.300 will be represented as:
$x + 2y = 300{\text{ }}...{\text{(1)}}$
$ \Rightarrow x = 300 - 2y{\text{ }}...{\text{(2)}}$
And the other equation for 2 bats and 3 balls of the same kind costing Rs.525 can be represented as:
$2x + 3y = 525{\text{ }}...{\text{(3)}}$
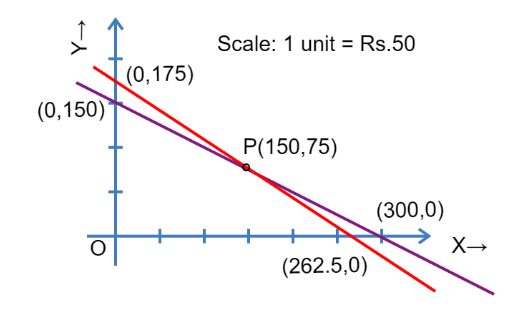
In graphical method: In this, we will substitute 2 to 3 values of y and get the table following for:
$x+2y = 300$
$2x + 3y = 525$
Now, putting the value of equation (2) in equation (3), we will get:
$
2(300 - 2y) + 3y = 525 \\
\Rightarrow y = 75 \\
$
And substituting the value of $y = 75$ in (2), we will get $x = 150$.
So, the coach will pay Rs.150 for a bat and Rs.75 for a ball.
Note: Whenever there are 2 equations in 2 variables, the easiest method to solve them is by the elimination method.
Put the value of one variable from one equation into the second equation to get the value of the second variable.
In the graph, the point at which both the lines are intersecting will give the values for x and y.
It can also be verified by solving the equations algebraically.
Complete step-by-step answer:
Let the cost of one bat be x rupees and the cost of one ball be y rupees.
In Algebraic form:
Then the equation for one bat and 2 balls costing Rs.300 will be represented as:
$x + 2y = 300{\text{ }}...{\text{(1)}}$
$ \Rightarrow x = 300 - 2y{\text{ }}...{\text{(2)}}$
And the other equation for 2 bats and 3 balls of the same kind costing Rs.525 can be represented as:
$2x + 3y = 525{\text{ }}...{\text{(3)}}$
In graphical method: In this, we will substitute 2 to 3 values of y and get the table following for:
$x+2y = 300$
| x | 0 | 300 |
| y | 150 | 0 |
$2x + 3y = 525$
| x | 0 | 262.5 |
| y | 175 | 0 |

Now, putting the value of equation (2) in equation (3), we will get:
$
2(300 - 2y) + 3y = 525 \\
\Rightarrow y = 75 \\
$
And substituting the value of $y = 75$ in (2), we will get $x = 150$.
So, the coach will pay Rs.150 for a bat and Rs.75 for a ball.
Note: Whenever there are 2 equations in 2 variables, the easiest method to solve them is by the elimination method.
Put the value of one variable from one equation into the second equation to get the value of the second variable.
In the graph, the point at which both the lines are intersecting will give the values for x and y.
It can also be verified by solving the equations algebraically.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What is the difference between rai and mustard see class 8 biology CBSE

Explain Mahalwari system class 8 social science CBSE




