Question

The coach of a cricket team buys 3 bats and 6 balls for Rs. 3900 Later, she buys another bat and 3 more balls of the same kind for Rs. 1300. Represent this situation algebraically and geometrically

Answer 1

Hint: In order to deal with this question first we have to assume cost of one bat and cost of one ball as a variable further according to the given statement we will make $2$ equations with $2$ variables at last by taking different values we will plot the graph.

Complete step-by-step answer:
Let us assume the cost of one bat be Rs. x
and the cost of one ball be Rs. y

Given that 3 bats and 6 balls cost Rs. 3900

It means 3 times the cost of one bat + 6 times the cost of one ball = 3900

Substitute the value of cost of one bat and one ball in above equation, we have

3x + 6y = 3900
3x + 6y – 3900 = 0 (equation 1)
It is also given that 1 bat and 3 balls cost Rs. 1300
Or we can write it as
1 time the cost of one bat + 3 times the cost of one ball = 1300
Substitute the value of cost of one bat and one ball in above equation, we have
x + 3y = 1300
Further by solving it we have
x + 3y - 1300 = 0 (equation 2)
multiplying the equation 2 by 3 and equation 1 by 1 and then subtracting equation 2 by equation 1 we get
3x + 9y – 3900 – 3x – 6y + 3900 = 0
3y = 0
y = 0
substituting the value of y in the equation 1 we get
x + 3 (0) - 1300 = 0
x = 1300
Therefore Rs. 1300 is the price of bat and Rs. 0 is the price of ball
As we can write equation 1 as
3x + 6y – 3900 = 0
y = $\dfrac{{3900 - 3x}}{6}$ (equation 3)
Now we will put the value of x = 0, 100, and 200 to get the corresponding value of y
Let us put x = 0
$y = \dfrac{{3900 - 3\left( 0 \right)}}{6} = \dfrac{{3900}}{6} = 650$
So, x = 0, y = 650 is a solution, i.e. (0,650) is a solution 
Now, let us put x = 100
$y = \dfrac{{3900 - 3\left( {100} \right)}}{6} = \dfrac{{3600}}{6} = 600$
So, x = 100, y = 600 is a solution, i.e. (100,600) is a solution 
Let put x = 200
$y = \dfrac{{3900 - 3\left( {200} \right)}}{6} = \dfrac{{3300}}{6} = 550$
So, x = 200, y = 550 is a solution, i.e. (200,550) is a solution 
Now solving equation 2, we get
x + 3y - 1300 = 0
3y = 1300 - x
$y = \dfrac{{1300 - x}}{3}$
Now substituting the value of x as 0, 100, and 200 to find the values of y
For x = 0
$y = \dfrac{{1300 - 0}}{3} = \dfrac{{1300}}{3} = 433.33$
So, x = 0, y = 433.33 is a solution, i.e. (0, 433.33) is a solution 
For x = 100
$y = \dfrac{{1300 - 100}}{3} = \dfrac{{1200}}{3} = 400$
So, x = 100, y = 400 is a solution, i.e. (100, 400) is a solution 
For x = 200
$y = \dfrac{{1300 - 200}}{3} = \dfrac{{1100}}{3} = 366.67$
So, x = 200, y = 366.67 is a solution, i.e. (200, 366.67) is a solution
Therefore, the values are (0, 433.33), (100, 400) and (200, 366.67)
Now plotting the values in the graph

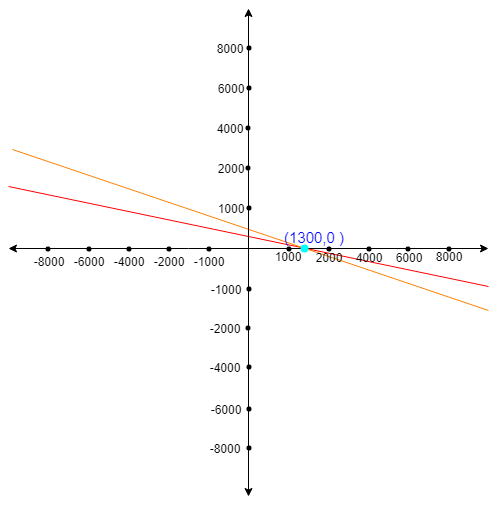
Note: In mathematics, a linear equation is an equation that may be put in the form where are the variables, and are the coefficients, which are often real numbers. The coefficients may be considered as parameters of the equation, and may be arbitrary expressions, provided they do not contain any of the variables.