Question

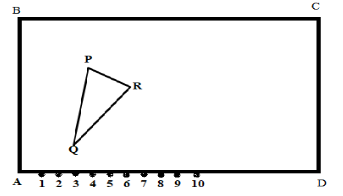
The class $X$ student of a secondary school in Krishinagar has been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar Are planted on the boundary at a distance of $1$m from each other. There is a triangular grassy lawn in the plot as shown in the fig. The students are to sow seeds of flowering plants on the remaining area of the plot.
$(i)$ Taking, A as origin, find the coordinates of the vertices of the triangle.
$(ii)$ What will be the coordinates of the vertices of $\Delta PQR$ it $C$ is the origin?
Also calculate the area of the triangles in these cases. What do you observe?

Answer 1

Hint: First we have to find out the vertices of axes by the given figure
By using the below formula to calculate
Area of triangle=$\dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
Then compare both the cases.
We will get the result.

Complete step-by-step answer:
 First of all we are drawing the above figure, as in the given figure:

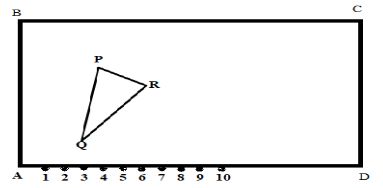
\[\left( i \right)\]While taking $A$ as origin
We have to find the coordinates of the vertices of $\Delta PQR$
Now we take that $AD$ is $X - $axis and $AB$ is the $Y - $axis.
Hence we can write the coordinates of the vertices of $\Delta PQR$ is
$P = (4,6)$,$Q = (3,2)$and $R = (6,5)$
\[\left( {ii} \right)\]If we take $C$ as origin
We have to find the coordinates of the vertices of $\Delta PQR$
Now we take that $CB$ is $X - $axis and $CD$ is the $Y - $axis.
Then the coordinates of the vertices of $\Delta PQR$ is
$P = (12,2),Q = (13,6),R = (10,3)$
Finally we have to find, \[\left( i \right)\]
Area of the triangle $PQR$= $\dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
Here the vertices are $P = (4,6)$,$Q = (3,2)$and $R = (6,5)$
Now we can write it as,
\[\left( {{x_1},{y_1}} \right) = \left( {4,6} \right)\]
\[\left( {{x_2},{y_2}} \right) = \left( {3,2} \right)\]
\[\left( {{x_3},{y_3}} \right) = \left( {6,5} \right)\]
Substitute the vertices in the formula we get,
$ = \dfrac{1}{2}\left[ {4(2 - 5) + 3(5 - 6) + 6(6 - 2)} \right]$
On some simplification we get,
 =$\dfrac{1}{2}\left[ { - 12 - 3 + 24} \right]$
Let us add the terms we get,
 =$\dfrac{9}{2}$sq. unit
Also we have to find $(ii)$:
Area of triangle $PQR$=$\dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
Here the vertices are $P = (12,2),Q = (13,6),R = (10,3)$
Now we can write it as,
\[\left( {{x_1},{y_1}} \right) = \left( {12,2} \right)\]
\[\left( {{x_2},{y_2}} \right) = \left( {13,6} \right)\]
\[\left( {{x_3},{y_3}} \right) = \left( {10,3} \right)\]
Substitute the vertices in the formula we get
 $ = \dfrac{1}{2}\left[ {12(6 - 3) + 13(3 - 2) + 10(2 - 6)} \right]$
On subtract the bracket terms we get,
$ = \dfrac{1}{2}\left[ {12 \times 3 + 13 \times 1 + 10( - 4)} \right]$
Multiply the values we get,
$ = \dfrac{1}{2}\left[ {36 + 13 - 40} \right]$
Let us add the values we get,
 =$\dfrac{9}{2}{\text{sq}}{\text{.unit}}$
Hence we get the required area of the triangle.
Here we observed that the area of triangle in both the cases is equal
So, it means that the area of any figure does not depend on the reference which you have taken.

Note: The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle.
If the area comes out to be zero, it means the three points are collinear.
So they lie in a straight line and do not form a triangle.