Question

The circumcentre of a triangle lies at the origin and it’s centroid is the midpoint of the line segment joining the points $\left( {{a}^{2}}+1,{{a}^{2}}+1 \right)$ and $\left( 2a,-2a \right)$,$a\ne 0$ . Then for any a, the orthocenter of this triangle lies on the line:

A) \[y-2ax=0\]
B) $y\left( {{a}^{2}}+1 \right)-x=0$
C) \[y+x\text{ }=0\]
D) \[{{\left( a-1 \right)}^{2}}x-{{\left( a+1 \right)}^{2}}y\text{ }=0\]

Answer 1

Hint: We know that circumcentre is the intersection point of all the perpendicular bisectors and centroid is intersection point of all the medians of the given triangle and orthocenter is the intersection of all angular bisectors of the given triangle. These points i.e. circumcentre, centroid and orthocenter are always collinear.

Complete step by step answer:
Given that the circumcentre(C) of triangle XYZ is origin which implies C = (0,0)
Also Given that the centroid (G) is the midpoint of the line segment joining the points E$\left( {{a}^{2}}+1,{{a}^{2}}+1 \right)$and F$\left( 2a,-2a \right)$ as shown in the diagram.

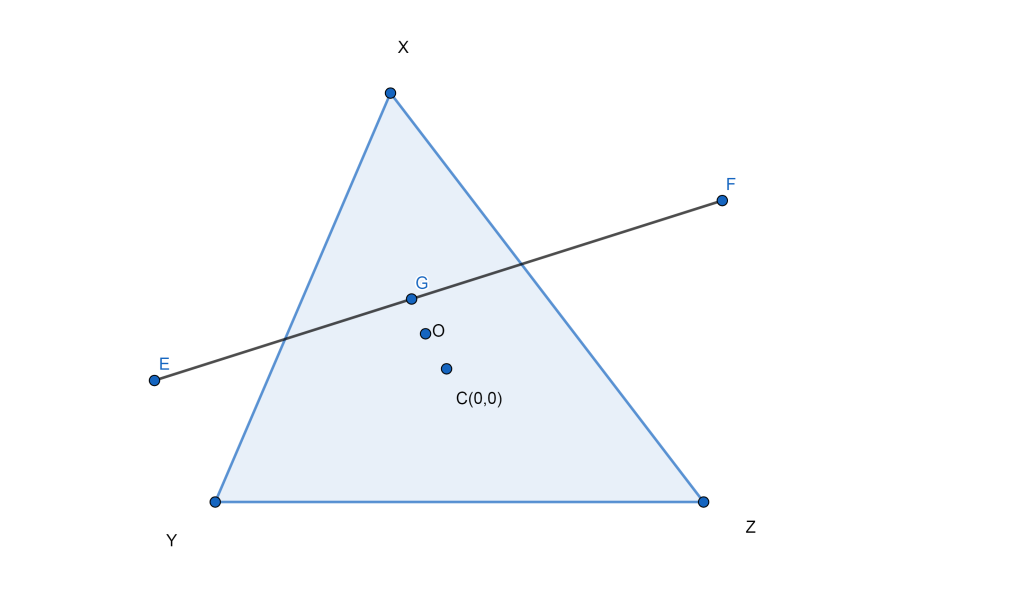
We know that midpoint of any two points(a,b) and (c,d) is ($\dfrac{a+c}{2},\dfrac{b+d}{2}$ )
which implies the centroid (G) = ($\dfrac{{{a}^{2}}+1+2a}{2},\dfrac{{{a}^{2}}+1-2a}{2}$) = ($\dfrac{{{(a+1)}^{2}}}{2},\dfrac{{{(a-1)}^{2}}}{2}$ )
[We already know that \[{{(a\pm b)}^{2}}=\text{ }{{a}^{2}}+{{b}^{2}}\pm 2ab\] ]
As we know that centroid , circumcentre , orthocenter are collinear , we can find the line that passes through these three points even when we know any of these two points.
So, now we will find the line passing through G and C so that the orthocenter lies on it.
We know that the equation of line that passes through (a,b) and (c,d) is
$\dfrac{y-b}{x-a}=\dfrac{d-b}{c-a}$
which implies the line passing through G ($\dfrac{{{(a+1)}^{2}}}{2},\dfrac{{{(a-1)}^{2}}}{2}$ ) and C(0,0) will be
$\dfrac{y-0}{x-0}=\dfrac{{{(a-1)}^{2}}/2-0}{{{(a+1)}^{2}}/2-0}$ ;
Which implies $\dfrac{y}{x}=\dfrac{{{(a-1)}^{2}}}{{{(a+1)}^{2}}}$;
Which implies \[{{\left( a+1 \right)}^{2}}y\text{ }=\text{ }{{\left( a-1 \right)}^{2}}x\] ;
That is also equal to \[{{\left( a-1 \right)}^{2}}x-{{\left( a+1 \right)}^{2}}y\text{ }=0\]

Therefore the orthocenter of this triangle lies on the line \[{{\left( a-1 \right)}^{2}}x-{{\left( a+1 \right)}^{2}}y\text{ }=0\]

So, the correct answer is “Option D”.

Note:
Go through the properties of all the circles and centres corresponding to the triangle that is orthocenter , centroid, circumcenter , incenter and find the ratios through which one center cuts the other .Also check the collinearities between them. Do not draw the graph whenever you see a question related to these centers. First read the total question and then solve the problem.