Question

The circuit shown here has two batteries of 8.0 V and 16.0 V and three resistors $3\Omega $, $9\Omega $ and $9\Omega $ with a capacitor $5.0\mu F$. The current I in the circuit at steady state is:

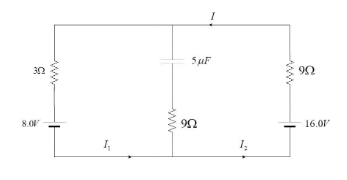
A. 1.6 A
B. 0.67 A
C. 2.5 A
D. 0.25 A

Answer 1

Hint: This problem should be solved with the help of Kirchhoff’s voltage law which states that the algebraic sum of the voltage drops in a closed loop is equal to the total emf in the loop.
$\sum V = 0$

Complete step-by-step answer:
Consider the circuit given here:

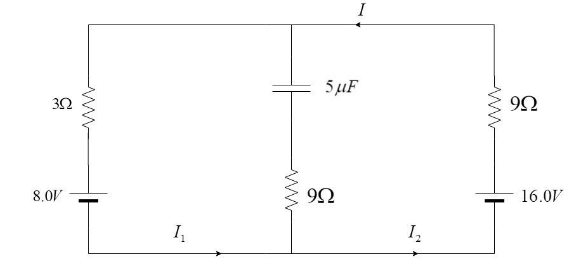
In the question, it is mentioned that the current is steady state. Steady state current means direct current. The capacitor offers infinite resistance to the flow of DC current. Hence, there is no current flowing through the middle branch.
Also, ${I_1} = {I_2} = I$
The modified circuit looks like this:

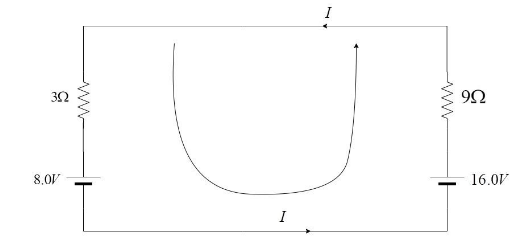
Applying Kirchhoff’s Voltage law for this mesh, we have –
$ - 3 \times I - 8 + 16 - 9 \times I = 0$
Rearranging and solving, we get –
$
  8 + 3I = 16 - 9I \\
   \to 12I = 8 \\
   \to 12I = 8 \\
   \to I = \dfrac{8}{{12}} = 0.667A \approx 0.67A \\
 $
Hence, the current in the circuit in the steady state, $I = 0.67A$

Hence, the correct option is Option B.

Note: At this point, you may be wondering the reason as to why the capacitor has blocked the DC current. Here is the reason:
Consider an A.C current passing through the capacitor. When the current passes through a capacitor, it obstructs the flow of the AC current through it. This property of the capacitor to obstruct the flow of current through it is called reactance.
Capacitive reactance, ${X_c} = \dfrac{1}{{\omega C}}$
where $\omega $ is called the angular frequency of the current and C is the capacitor.
The value of $\omega = 2\pi f$
If the current is DC, the frequency $f = 0 \to \omega = 0$
Substituting, we get –
${X_c} = \dfrac{1}{{\omega C}} = \dfrac{1}{0} = \infty $
Here, we can see that the reactance is infinity, which means a very high value. With such high values of reactance, it does not completely allow the direct current to pass through it.
Hence, it proves that the capacitor blocks DC current.