Question

The centroid of the triangle divides each median in the ratio __________
A) 1:1
B) 2:3
C) 2:1
D) 3:1

Answer 1

Hint: Draw the figure of the triangle along with the median and Centroid an also the reflection of it and draw the figure in such a way that the length from one vertex of the triangle to the centroid is equal to another vertex of the reflection of triangle to the same centroid of the previous triangle.
Complete step by step answer:
 First of all let us draw the figure which will be required to prove the relation

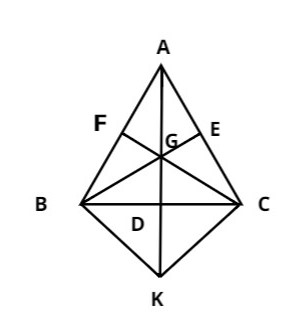
Now Here G is the centroid of the triangle and AD, BE, CF are the medians.
Construction: Produce AD to K such that \[AG = GK\] , join BK and CK
In \[\vartriangle ABK,\]
F and G are midpoints of AB and AK respectively
So, \[FG||BK\] (by the midpoint theorem)
Hence we can say that \[GC||BK.....................(i)\]
In \[\vartriangle AKC,\]
Similarly, \[KC||BG.....................(ii)\]
Now by equation (i) and (ii), we can say that
BGCK is a parallelogram
In a parallelogram diagonals bisect each other
\[\therefore GD = DK....................(iii)\]
\[AG = GK\] [ by construction]
\[\begin{array}{l}
AG = GD + DK\\
So,AG = 2GD\\
 \Rightarrow \dfrac{{AG}}{{GD}} = \dfrac{2}{1}
\end{array}\]
 Thus, the centroid of the triangle divides each of the median in the ratio 2:1.
Therefore, Option (C) is correct.

Note: Always write the property you are using while writing any proof in geometry if its a theorem also then mention it in a bracket nearby This leaves a good impact on the examiner and also helps to make your answer more understandable and proper.