Question

The centre, one vertex and one focus of a hyperbola are (1,-1), (5,-1) and (6,-1) respectively. The equation of its directrix are:
A. 5x-21=0, 5x+11=0
B. 5x+4=0, x+1=0
C. 5x-7=0, 5x-19=0
D. 5x-17=0, 5x-6=0

Answer 1

Hint: Apply the general equation of the directrix and also find the distance between centre and vertex of hyperbola to solve the question.Directrix of hyperbola, It is the straight line that is used in generating curves. It can also be defined as the line from which the hyperbola curves away from. The line is perpendicular to the axis of symmetry. In the given question, the distance between the centre and vertex, also distance between center and focus has to be found, then the equation has been solved.

Complete step by step answer:
In the above question, find the distance between the center, and the vertex of hyperbola.
Firstly, let us know about the center of hyperbola. The centre of hyperbola is that in which the mid point of the line-segment joins its foci. The transverse axis is that line segment that contains the center of the hyperbola and where end points are two vertices of the hyperbola.

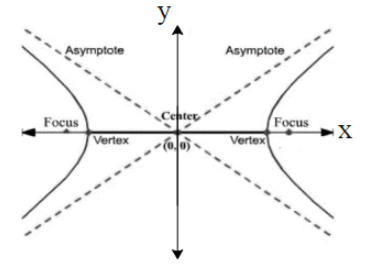
The other part of a hyperbola is the directrix of the hyperbola. Let us discuss about it,
The equation of directrix is
$x=\dfrac{\pm {{a}^{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
The standard form of hyperbola, If transverse axis is horizontal:
$\dfrac{{{(x-h)}^{2}}}{{{a}^{2}}}-\dfrac{{{(y-k)}^{2}}}{{{b}^{2}}}=1$ where ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$
In the given question:
The center of hyperbola is $\left( 1,-1 \right)$
The vertex of hyperbola is $\left( 5,-1 \right)$
The focus of hyperbola is $\left( 6,-1 \right)$
Since the axis of a hyperbola is parallel to x-axis. Let ‘a’ be the distance between centre and vertex, which is $4$. Let ‘b’ the be the distance between centre and focus, which is$~5$.
Also having,
$e=b/a~~~~$ i.e. $a=5/4$
Now general equation of distance with center at $\left( 0,0 \right)$is $r=a/e$
But in this case centre of hyperbola is shifted to $\left( 1,-1 \right)$
So, equation of the distance will be:
$x-1=a/c$ ………………equation(a)
and
$x-1=-(a/c)$ ………………….equation(b)
Substituting the values of a and e in the equation A, we get:
$x-1=a/c$
$\Rightarrow x-1=\dfrac{4}{5/4}$
$\Rightarrow x-1=16/5$
cross multiplying the above terms, we have:
$5x\text{ }-\text{ }5\text{ }=\text{ }16$
$\Rightarrow 5x-\text{ }5\text{ }\text{ }16\text{ }=\text{ }0$
$\Rightarrow 5x\text{ }-21\text{ }=\text{ }0$
Again, substituting the values of a and e in the equation B, we get:
$x-1=-(a/c)$
$\Rightarrow x-1=-\dfrac{4}{5/4}$
$\Rightarrow x-1=-16/5$
cross multiplying the above terms, we have:
$\Rightarrow 5x-5=-16$
$\Rightarrow 5x+11=0$

The equations of directrix are: $5x\text{ }-21\text{ }=\text{ }0$ and $5x+11=0$.

Note:The vertex of hyperbola is that in which the vertices are at some fixed distance from the centre. The line joining from one vertex through the centre and ending at the other vertex is called the transfer axis. The “foci” of a hyperbola are inside each branch and each focus is located some fixed distance” c” from the centre.In each hyperbola there are two most important points, called foci. The curve of hyperbola is defined as the set of all points that have the same distance between the distance to each focus.