Question

The centre of a square \[ABCD\] is at \[z=0\]. If \[A\] is \[{{z}_{1}}\], then the centroid of triangle \[ABC\] is
A. \[\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)\]
B. \[\dfrac{{{z}_{1}}}{3}\left( \cos \pi +i\sin \pi \right)\]
C. \[{{z}_{1}}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)\]
D. None of these

Answer 1

Hint: Centroid of a triangle divide the median in the ratio of 2:1. If the coordinates of the vertices of the triangle are given centroid is calculated as the sum of the coordinates divided by 3. The triangle \[ABC\] formed, is an isosceles triangle. We will also use the concept of rotation about the origin in a complex plane.

Complete step-by-step solution:
Let us consider the centroid of triangle \[ABC\] as G. And let the center of the square \[ABCD\] be O which is \[z=0\].

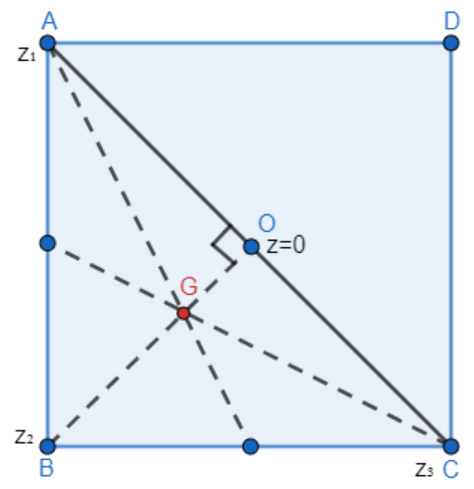
Now, in the square \[ABCD\]we have \[OA=OB=OC\].
We have been given that, \[A\] is \[{{z}_{1}}\]. So, let us consider \[B\] as \[{{z}_{2}}\] and \[C\] as \[{{z}_{3}}\].
So, we have, \[OA={{z}_{1}}-0\], \[OB={{z}_{2}}-0\] and \[OC={{z}_{3}}-0\].
We know that the diagonals of a square intersect at right angles.
We will use the rotation theorem for complex numbers. If we have two complex numbers, say ${{z}_{1}}\text{ and }{{z}_{2}}$ such that $\left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|$ and the angle of rotation in counter-clockwise direction from ${{z}_{2}}$ to ${{z}_{1}}$ is $\theta $ , then we can write that ${{z}_{2}}={{z}_{1}}{{e}^{i\theta }}$ .
Now, we will rotate \[OA\] by right angle to \[OB\] in a counter-clockwise direction. So, here we have ${{z}_{1}}=OA\text{ and }{{z}_{2}}=OB$ and $\theta ={{90}^{\circ }}=\dfrac{\pi }{2}$ . So, we can write it as
\[OB=OA{{e}^{i\dfrac{\pi }{2}}}\]
Now we have,
\[({{z}_{2}}-0)=({{z}_{1}}-0){{e}^{i\dfrac{\pi }{2}}}\]
\[{{z}_{2}}={{z}_{1}}{{e}^{i\dfrac{\pi }{2}}}\]…………………….. (i)
Similarly, when \[OA\] is rotated by \[{{180}^{\circ }}\] counter-clockwise to \[OC\] we can apply rotation theorem for ${{z}_{1}}=OA\text{ and }{{z}_{2}}=OC$ and $\theta ={{180}^{\circ }}=\pi $ as below,
\[OC=OA{{e}^{i\pi }}\]
Substituting values, we have
\[({{z}_{3}}-0)=({{z}_{1}}-0){{e}^{i\pi }}\]
\[{{z}_{3}}={{z}_{1}}{{e}^{i\pi }}\]……………………… (ii)
The centroid of the triangle \[ABC\] is given by G = \[\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3}\] ……………. (iii)
On putting the values of \[{{z}_{1}}\]and \[{{z}_{2}}\] from (i) and (ii) in (iii), we have
G = \[\dfrac{{{z}_{1}}+{{z}_{1}}{{e}^{i\dfrac{\pi }{2}}}+{{z}_{1}}{{e}^{i\pi }}}{3}\]
G = \[\dfrac{{{z}_{1}}}{3}\left( 1+{{e}^{i\dfrac{\pi }{2}}}+{{e}^{i\pi }} \right)\]
As we know that \[{{e}^{i\theta }}=\cos \theta +i\sin \theta \], we can write G as,
G = \[\dfrac{{{z}_{1}}}{3}\left( 1+\cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2}+\cos \pi +i\sin \pi \right)\]
We know that $\cos \pi =-1$ and $\sin \pi =0$. So, on applying this property, we will get,
G = \[\dfrac{{{z}_{1}}}{3}\left( 1+\cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2}-1+0 \right)\]
On simplifying further, we will get,
G = \[\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)\]
Hence, the centroid of the triangle \[ABC\] is G = \[\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)\].
Therefore, option A is correct.

Note: In this question, the concept which is very much important to keep in mind is the rotation of vector in a complex plane. Don’t get confused with the angle of rotation as we have done a counter-clockwise rotation in this particular problem so we get the answer \[\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)\], we may have also done the rotation in a clockwise direction and in that case the answer will be \[\dfrac{{{z}_{1}}}{3}\left( \cos \dfrac{\pi }{2}-i\sin \dfrac{\pi }{2} \right)\]. Also, the formula for the centroid of a triangle is important to solve these types of problems.