Question

The centre O of the smaller circle lies on the circumference of the bigger circle. If$\angle APB = 70^\circ and\angle BCD = 60^\circ $, find: (i) $\angle ADB.$

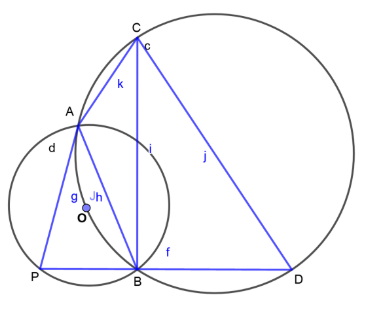
Answer 1

Hint: To solve this problem we will require two concepts which are, “Angle subtended by an arc at the centre is twice the angle subtended by the same arc at any point on the circumference” and “Opposite angles of a cyclic quadrilateral are always Supplementary i.e. their summation is”.

Complete step-by-step answer:
We will write the given values first,
$\angle APB = 70^\circ and \angle BCD = 60^\circ $………………………….. (1)
To get the answer we have to make required changes/constructions in the figure.
As follows,
1)Join AO and BO to get $\angle AOB$.
2)Join AD to get $\angle ADB.$.

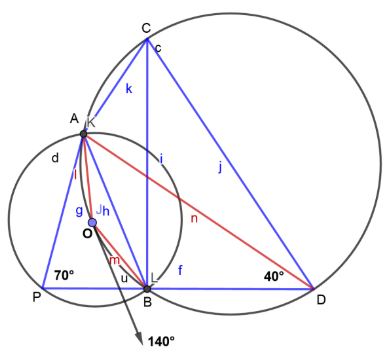
To find the value of $\angle AOB$ we should know the concept given below,
Concept: Angle subtended by an arc at the centre is twice the angle subtended by the same arc at any point on the circumference.
Which means if we consider the smaller circle with centre O then by above concept,
Angle subtended by an arc AB at centre ($\angle AOB$) is twice the angle subtended by it at point P on the circle ($\angle APB$).
$\therefore \angle AOB = 2\angle APB$
$\therefore \angle AOB = 2 \times 70^\circ $ [From (1)]
$\therefore \angle AOB = 140^\circ $ -(2)
Now, consider the bigger circle in which $\square AOBD$ is a cyclic quadrilateral,
Here comes the last concept which gives the final answer,
Concept: Opposite angles of a cyclic quadrilateral are always
Supplementary i.e. their summation is $180^\circ $.

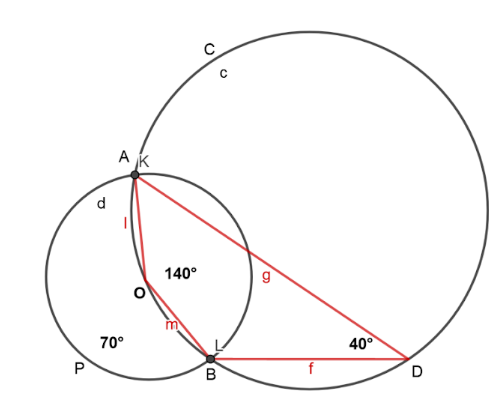
As $\angle AOB and \angle ADB$ are opposite angles of cyclic quadrilateral,
$\angle AOB + \angle ADB = 180^\circ $
$140^\circ + \angle ADB = 180^\circ $ [From (2)]
$\angle ADB = 180^\circ - 140^\circ $
$\angle ADB = 40^\circ $
Therefore, the value of $40^\circ $ $\angle ADB$ is $40^\circ $.

Note: Try to simplify the solution by drawing simplified diagrams; it will increase your accuracy. Use the property of cyclic quadrilateral and angle subtended by the arc of the circle.