Question

The central angle and radius of a sector of a circular disc are ${{180}^{\circ }}$ and 21 cm respectively. If the edges of the sector are joined together to make a hollow cone, then find the radius of the cone.

Answer 1

Hint: Closely observing the sector is actually a semicircle and its circumference is equal to the base of cone

Complete step-by-step answer:

In the question, data given is a circular disc with central angle 180 degrees and radius 21 cm.
As we know the central angle of the sector, we will derive the formula of circumference of sector by using the formula,


Circumference of Sector = $\dfrac{\theta }{360}\times 2\pi r$

where $\theta $ is the central angle given and r is the radius of the sector.

So, the circumference is $\begin{align}

  & =\dfrac{180}{360}\times 2\pi r \\

 & =\dfrac{1}{2}\times 2\pi r \\

 & =\pi r \\

\end{align}$

So, the circumference of the sector is $=\dfrac{22}{7}\times 21cm=66cm$

Now the sector is transformed into a hollow cone which is represented in fig 1 and fig 2 respectively

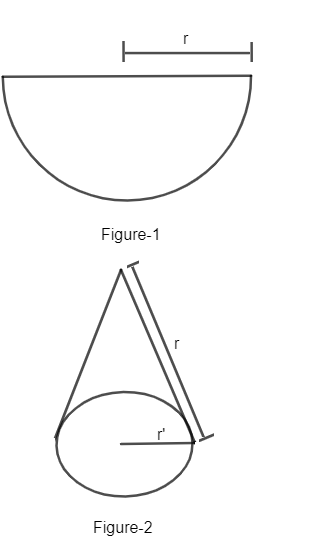
The cone formed after the transformation let the radius of the circular base of the cone be $r'$ . Then the circumference of the base of the cone will be $2\pi r'$ .The radius of the sector will become slant height l of the cone.

So,

\[\begin{align}

  & 2\pi r'=66 \\

 & \Rightarrow 2\times \dfrac{22}{7}\times r'=66 \\

 & \Rightarrow r'=\dfrac{1}{2}\times \dfrac{7}{22}\times 66 \\

 & \text{ }=10.5cm \\

\end{align}\]

Hence the radius of the hollow cone is 10.5 cm.

Note: In this type of question if any other angle would be given, then we should use perimeter = $\dfrac{\theta }{360}\times 2\pi r$ where $\theta $ is angle of sector.