Question

The center of mass of a non uniform rod of length L whose mass per unit length varies as $\rho = k{x^2}/L$ (where $k$ is a constant and $x$ is the distance measured from one end) is at what distance from the same end?
$\eqalign{
  & {\text{A}}{\text{. }}\dfrac{{3L}}{4} \cr
  & {\text{B}}{\text{. }}\dfrac{L}{4} \cr
  & {\text{C}}{\text{. }}\dfrac{{2L}}{3} \cr
  & {\text{D}}{\text{. }}\dfrac{L}{3} \cr} $

Answer 1

Hint: Center of mass is a unique point in space such that the mass of a particle is equivalent to the mass of a given object for application of Newton’s laws of motion. The center of mass for a non- uniform rod can be calculated by first forming the equation for its mass using a small element and integrating its mass to get the mass of the entire rod. Later find the center of mass using its mathematical equation.

Formula used:
The center of mass of a body is given as:
${x_{COM}} = \dfrac{1}{M}\int {dm.x} $

Complete step by step answer:
The center of mass of a body is defined as a point on the body where the distribution of its entire mass when weighted relative to their respective position, the sun comes out to be zero. In other words, it is a unique point in space such that the entire mass of an object is equivalent to a point particle.
Mathematically, it is given as:
${x_{COM}} = \dfrac{1}{M}\int {dm.x} $
Given:
Length of the non-uniform rod =L
Mass per unit length of the rod, $\rho = k{x^2}/L$
Consider a small element dx, having mass dm at a distance x from the left side of the rod as shown in the diagram below:

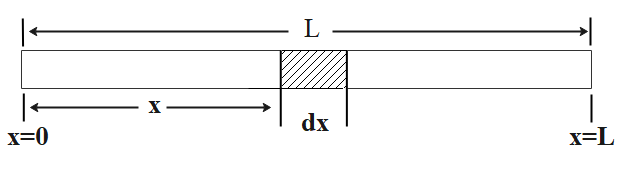
Now, the mass of the small element dm will be given by:

$\eqalign{
  & dm = \rho dx \cr
  & dm = \dfrac{{k{x^2}}}{L}dx \cdots \cdots \cdots \cdots \left( 1 \right) \cr} $
So, the total mass of the rod will be:
$\eqalign{
  & \int {dm} = \int\limits_0^L {\dfrac{{k{x^2}}}{L}dx} \cr
  & \int {dm} = \dfrac{k}{L}\int\limits_0^L {{x^2}dx} \cr
  & M = \dfrac{k}{L}\left| {\dfrac{{{x^3}}}{3}} \right|_0^L \cr
  & M = \dfrac{k}{L} \times \dfrac{{{L^3}}}{3} \cr
  & M = \dfrac{{k{L^2}}}{3} \cdots \cdots \cdots \cdots \cdots \left( 2 \right) \cr} $
Now, the center of mass of rod is located at
${x_{COM}} = \dfrac{1}{M}\int {dm.x} {\text{ }} \cdots \cdots \cdots (3)$
Substituting values from equation (1) into equation (3), we get:
$\eqalign{
  & {x_{COM}} = \dfrac{1}{M}\int\limits_0^L {\dfrac{{k{x^2}}}{L}} \times xdx \cr
  & {x_{COM}} = \dfrac{1}{M}\int\limits_0^L {\dfrac{{k{x^3}}}{L}} dx \cr
  & {x_{COM}} = \dfrac{1}{M}\left( {\dfrac{{k{L^4}}}{{4L}}} \right) \cr} $
Putting the value of M from equation (2), we get:
$\eqalign{
  & {x_{COM}} = \dfrac{1}{M}\left( {\dfrac{{k{L^4}}}{{4L}}} \right) \cr
  & {x_{COM}} = \dfrac{3}{{k{L^2}}}\left( {\dfrac{{k{L^4}}}{{4L}}} \right) \cr
  & {x_{COM}} = \dfrac{{3L}}{4} \cr} $
Therefore, the correct option is A. i.e., The center of mass of a non-uniform rod of length L whose mass per unit length varies as $\rho = k{x^2}/L$ is at $\dfrac{{3L}}{4}$ from the same end.

Note:
Suppose a particle has its center of mass at ${C_1}$ and its total mass is ${M_1}$. Similarly, another particle has a center of mass at ${C_2}$ and its total mass is ${M_2}$. If ${X_1},{\text{ }}{X_2}$ are the x-coordinates of ${C_1}{\text{ and }}{C_2}$ respectively, then by definition of center of mass, we have:

$X = \dfrac{{{M_1}{X_1} + {M_2}{X_2}}}{{{M_1} + {M_2}}}$
Similarly, $Y = \dfrac{{{M_1}{Y_1} + {M_2}{Y_2}}}{{{M_1} + {M_2}}}$
And $Z = \dfrac{{{M_1}{Z_1} + {M_2}{Z_2}}}{{{M_1} + {M_2}}}$

But this is also the center of mass of two point particles of masses ${M_1}{\text{ and }}{M_2}$ placed at ${C_1}{\text{ and }}{C_2}$ respectively. Thus, if we know the center of mass of parts of the system and their masses, we can get the combined center of mass by treating the parts as point particles placed at their respective center of masses.