Question

The cartesian equation of a line is $6x-2=3y+2=2z-2$. Find its direction ratios and also find the vector equation of the line.

Answer 1

Hint: First of all, express the given line in the form of standard line, that is, $\dfrac{x-a}{m}=\dfrac{y-b}{n}=\dfrac{z-c}{p}$. Now for this line, $\left( m,n,p \right)$ are its direction ratios. Also, the vector equation of a line is given as $\overset{\to }{\mathop{r}}\,=a\widehat{i}+b\widehat{j}+c\widehat{k}+\lambda \left( m\widehat{i}+n\widehat{j}+p\widehat{k} \right)$.

Complete step-by-step answer:
We are given a cartesian equation of a line as $6x-2=3y+2=2z-2$. We have to find its direction and the vector equation of the line. Before proceeding with the question, let us loot at what vector ratios mean. When a directed line $OP$ passing through the origin makes $\alpha ,\beta $ and $\gamma $ angles with $x,y$ and $z$ axis respectively with 0 as reference, then these angles are referred to as the direction angles of line and cosine of these angles give us the direction cosines. These direction cosines are usually represented as $l,m$ and $n$. Now, when these direction cosines are multiplied by a particular number, then the new ratios $\left( a,b,c \right)$ are called as direction ratios of line.

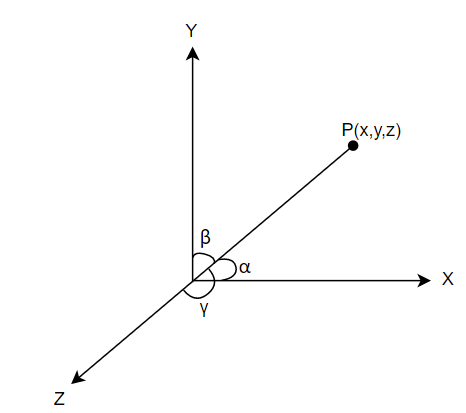
Now, let us consider our question. We are given the cartesian equation of a line as, $6x-2=3y+2=2z-2$. We know that for the line of a standard form $\dfrac{x-a}{m}=\dfrac{y-b}{n}=\dfrac{z-c}{p}$, the line passes through $\left( a,b,c \right)$ and its direction ratios are $\left( m,n,p \right)$. So, first, let us convert the given line in this form.
$6x-2=3y+2=2z-2$
By taking out $6,3,2$, which are the common from the first, second and third term of the above equation respectively, we get,
$\begin{align}
  & 6\left( x-\dfrac{2}{6} \right)=3\left( y+\dfrac{2}{3} \right)=2\left( z-\dfrac{2}{2} \right) \\
 & \Rightarrow 6\left( x-\dfrac{1}{3} \right)=3\left( y-\left( \dfrac{-2}{3} \right) \right)=2\left( z-1 \right) \\
\end{align}$
By dividing by 6 in the above equation, we get,
$\begin{align}
  & \dfrac{6\left( x-\dfrac{1}{3} \right)}{6}=\dfrac{3\left( y-\left( \dfrac{-2}{3} \right) \right)}{6}=\dfrac{2\left( z-1 \right)}{6} \\
 & \Rightarrow \dfrac{\left( x-\dfrac{1}{3} \right)}{1}=\dfrac{y-\left( \dfrac{-2}{3} \right)}{2}=\dfrac{\left( z-1 \right)}{3} \\
\end{align}$
Now, as we have expressed our line in standard form $\dfrac{x-a}{m}=\dfrac{y-b}{n}=\dfrac{z-c}{p}$, we get,
direction ratios of given line $=\left( m,n,p \right)=\left( 1,2,3 \right)$. Line passes through the points $=\left( a,b,c \right)=\left( \dfrac{1}{3},\dfrac{-2}{3},1 \right)$. Now, we know that if a line passes through points $\left( a,b,c \right)$ and its direction ratios are $\left( m,n,p \right)$, then its vector equation is given by, $\overset{\to }{\mathop{r}}\,=a\widehat{i}+b\widehat{j}+c\widehat{k}+\lambda \left( m\widehat{i}+n\widehat{j}+p\widehat{k} \right)$
By substituting $a=\dfrac{1}{3},b=\dfrac{-2}{3},c=1$ and $m=1,n=2,p=3$ in the above equation, we get the vector equation of the given line as, $\overset{\to }{\mathop{r}}\,=\dfrac{1}{3}\widehat{i}-\dfrac{2}{3}\widehat{j}+\widehat{k}+\lambda \left( \widehat{i}+2\widehat{j}+3\widehat{k} \right)$.
Hence, we get the direction ratios of the given line as $\left( 1,2,3 \right)$ and the vector equation as, $\overset{\to }{\mathop{r}}\,=\dfrac{1}{3}\widehat{i}-\dfrac{2}{3}\widehat{j}+\widehat{k}+\lambda \left( \widehat{i}+2\widehat{j}+3\widehat{k} \right)$.

Note: In this question, many students make mistake while converting the given line to the standard form, that is $\dfrac{x-a}{m}=\dfrac{y-b}{n}=\dfrac{z-c}{p}$. So be careful while taking out the common terms and putting the signs in the numbers. It is always better to convert the given line into a standard form of line other than remembering multiple formulas to calculate the direction ratios, etc.