Question

What will be the capacity of a bucket to fill the liquid which is $45$ cm high where the radii for both the ends of the bucket are $28$ cm and $7$ cm respectively?
(a) \[48400{\text{ }}c{m^3}\]
(b) \[4851{\text{ }}c{m^3}\]
(c) \[48490.5{\text{ }}c{m^3}\]
(d) None of these

Answer 1

Hint: The given problem revolves around the concepts of geometry of mensuration means to solve the required surface area, volume, etc. for the solid models used in day to day lifespan. Here, we will directly use the formula (due to all the given values known) for volume of frustum i.e. $\dfrac{\pi }{3}h\left[ {r_1^2 + r_2^2 + {r_1}{r_2}} \right]$ as it the shape of bucket tends to it respectively. As a result, substituting all the values provided, the desired capacity of the bucket is obtained.

Complete step-by-step answer:
Since, we have been given that to find the capacity (equals to its volume) of a bucket which is generally in the shape of “Frustum of Cone'' (is the cone when cut-off in solid geometry particularly. Also, known as Trapezium in $2D$ geometry)”

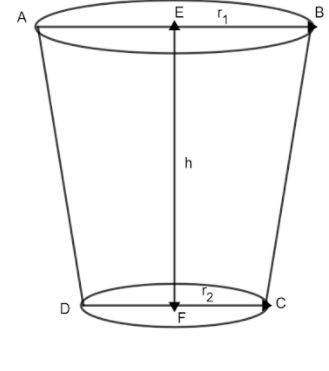
Consider the above rough figure (not drawn to scale)!
Figure ABCD is the frustum of bucket,
AB is the upper end of the bucket and CD is the lower end of the bucket having the radii for both the ends with height ‘$h$’ respectively.
As a result, we know that
To find the capacity that is volume of the bucket, we have
Volume of Bucket $ = $ Volume of Bucket $ = \dfrac{\pi }{3}h\left[ {r_1^2 + r_2^2 + {r_1}{r_2}} \right]$
Where, H is the height of the respective bucket $h = 45cm$,
${r_1}$ is the radius of the upper end of the bucket i.e. ${r_1} = 28cm$,
${r_2}$ is the radius of the lower end of the respective bucket ${r_2} = 7cm$.
Hence, substituting the given values in the formula for its volume, we get
\[Volume{\text{ }}of{\text{ }}Bucket = \dfrac{\pi }{3} \times 45cm\left[ {{{28}^2} + {7^2} + 28 \times 7} \right]c{m^2}\]
Solving the equation mathematically, we get
\[Volume{\text{ }}of{\text{ }}Bucket = \pi \times 15\left( {784 + 49 + 196} \right)c{m^3}\]
\[Volume{\text{ }}of{\text{ }}Bucket = \pi \times 15 \times 1029c{m^3}\]
Substituting the $\pi = \dfrac{{22}}{7}$ and then solving it, we get
\[Volume{\text{ }}of{\text{ }}Bucket = \dfrac{{22}}{7} \times 15 \times 1029c{m^3}\]
\[Volume{\text{ }}of{\text{ }}Bucket = 22 \times 15 \times 147c{m^3}\]
Hence, the required capacity of the bucket is,
\[Volume{\text{ }}of{\text{ }}Bucket = 48510c{m^3}\]
Since, no exact value exists from the given options provided to us!
$\therefore \Rightarrow $The option (d) is correct.
So, the correct answer is “Option d”.

Note: One must be able to know the formula to find the total surface areas, volume, perimeters, etc. for the solid (geometry) models such as cone, cylinder, frustum, cube, cuboid, sphere, etc. As a result, keeping in mind calculations need to be done logically such as taking the value of $\pi $ as $\dfrac{{22}}{7}$ instead of $3.14$, so as to be sure of our final answer.