Question

The ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ and ${{\text{F}}^ - }$ are located in ${\text{Ca}}{{\text{F}}_{\text{2}}}$crystal respectively at face-centred cubic lattice points and in
A. tetrahedral voids
B. half of tetrahedral voids
C. octahedral voids
D. half of octahedral voids

Answer 1

Hint: In a cubic lattice, one type of atoms or ions forms the crystal and the second type of atoms or ions are present in the voids. The unit cell has two types of voids, octahedral and tetrahedral. The number of voids depends upon the number of atoms or ions in a unit cell. We will determine the number of calcium ions. From this, we will determine the number of voids then based on the number of fluoride ions and voids we will decide the voids occupied by the fluoride ions.

Complete step-by-step answer:
It is given that ${\text{Ca}}{{\text{F}}_{\text{2}}}$forms face-centred cubic lattice in which ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ ions are located at face-centre lattice point.
The presence of ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ ions at face-centre lattice points is shown as follows:

The structure of a face-centered unit cell is as follows:

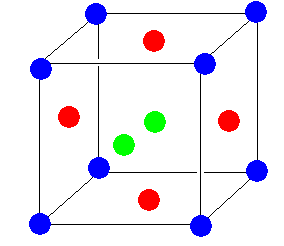
All the ions are the same (here, ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ ions) only for better understanding atoms are shown in different colours. The blue ions are at the corners. One green is on the face which is in front of us. One is on the face which is just opposite of the front. Four blue are on the remaining faces.

A face centered cubic unit cell has eight ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ ions at each corner and six ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ ions at each face. The ions present at the corner contribute $1/8$ in the unit cell and the ions present at face centre contribute $1/2$ in the unit cell. So, a total ions are,
${\text{ = }}\,\left( {{\text{1/8}}\, \times \,8} \right)\, + \left( {\,{\text{1/2}}\, \times \,{\text{6}}} \right)$
$ = \,4$

So, in the face centered cubic lattice four ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ ions are present.The formula of number of voids is as follows:

Tetrahedral voids = ${\text{2n}}$
Octahedral void = n
Where,
n is the number of atoms in a unit cell.

So, in the face centered cubic lattice of ${\text{Ca}}{{\text{F}}_{\text{2}}}$ the number of tetrahedral void is eight and number of octahedral void is four.

Now, according to the formula of calcium fluoride${\text{Ca}}{{\text{F}}_{\text{2}}}$, we can say that the number of fluoride ions are double of number of calcium ions.

So, as the number of ${\text{C}}{{\text{a}}^{{\text{2 + }}}}$ is four so, the number of ${{\text{F}}^ - }$ ions will be eight.

So, eight fluoride ions will occupy eight tetrahedral voids.

So, the $Ca^{2+}$ and ${{\text{F}}^ - }$ are located in ${\text{Ca}}{{\text{F}}_{\text{2}}}$crystal respectively at face-centred cubic lattice points and in tetrahedral voids.

Therefore, option (A) tetrahedral voids is correct.

Note: The face centered cubic unit cell always has four octahedral and eight tetrahedral voids. In a face-centered cubic unit cell, two tetrahedral void is present at\[\dfrac{{\sqrt {\text{3}} {\text{a}}}}{{\text{4}}}\,\] distance from corner. When three atoms are placed in a triangular plane, a cavity is formed and then we place an atom on this cavity a tetrahedral void forms. When we place four atoms in a plane and two atoms above and below the plane, the formed cavity is known as an octahedral void.