Question

The bond order of $C_{2}^{+}$ is
(A) 1
(B) 2
(C) $\dfrac{3}{2}$
(D) $\dfrac{1}{2}$

Answer 1

Hint: To solve this question, we first need to know what is bond order. The number of chemical bonds through which a pair of atoms are bonded is known as the bond order. The bond order of a molecule can be determined through the concept of molecular orbital theory.

Complete answer:
Now, to determine the bond order of $C_{2}^{+}$, we first need to draw its molecular orbital diagram.

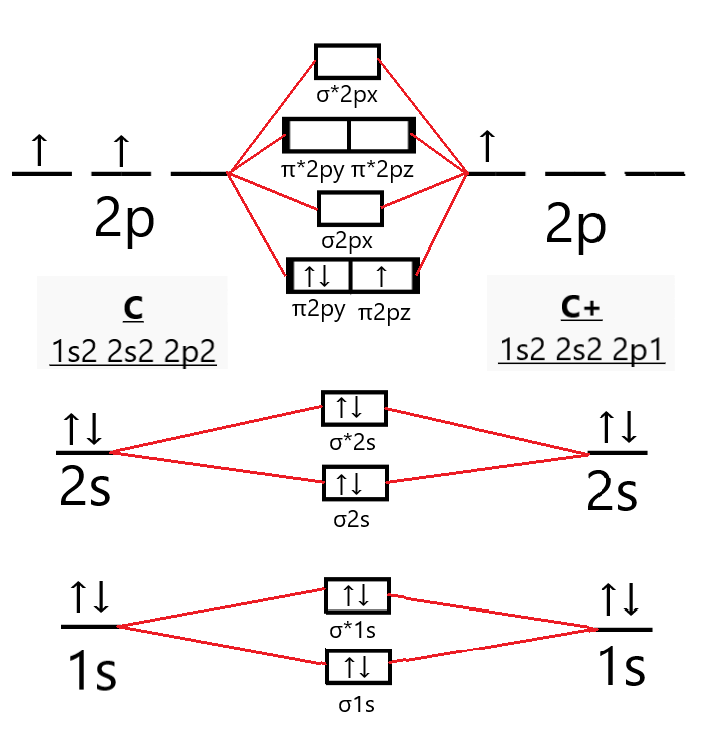
So, the electronic configuration of the $C_{2}^{+}$ molecule according to the molecular orbital theory is
\[C_{2}^{+}={{(\sigma 1s)}^{2}}{{(\sigma *1s)}^{2}}{{(\sigma 2s)}^{2}}{{(\sigma *2s)}^{2}}{{(\pi 2py)}^{2}}{{(\pi 2pz)}^{1}}\]
Where $\sigma /\pi $ orbitals depict bonding molecular orbitals whereas $\pi */\sigma *$ depict antibonding molecular orbitals.
Now, the bond order of a molecule is given by the formula
\[BO=\dfrac{1}{2}[{{N}_{b}}-{{N}_{a}}]\]
Where the number of electrons in the bonding orbitals is denoted by ${{N}_{b}}$ and the number of electrons in the antibonding orbitals is denoted by ${{N}_{a}}$.
From the molecular orbital diagram of the $C_{2}^{+}$ molecule we can see that it has 7 electrons in its bonding orbitals (${{N}_{b}}$) and 4 electrons in its antibonding orbitals (${{N}_{a}}$).
So, its bond order will be
\[\begin{align}
  & B{{O}_{C_{2}^{+}}}=\dfrac{1}{2}[7-4] \\
 & B{{O}_{C_{2}^{+}}}=\dfrac{3}{2} \\
\end{align}\]

Hence the correct answer is option (C) $\dfrac{3}{2}$.

Additional Information:
When a molecule has an unpaired electron in its orbital, it has a net spin value and hence is paramagnetic.
Whereas if a molecule does not have an unpaired electron in its orbital, it has a 0 net spin value and hence is diamagnetic.
In $C_{2}^{+}$, the $\pi 2pz$ orbital has an unpaired electron; hence the molecule is paramagnetic.

Note:
It should be noted that the stability of a bond can be indicated by bond order. The higher the bond order of a molecule, the more the atoms are held together tightly due to an increase in attraction between its electrons.