Question

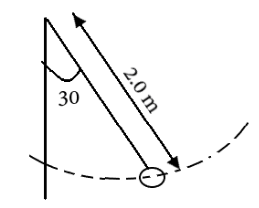
The bob of the pendulum shown in figure describes an arc of a circle in a vertical plane. If the tension in the cord is $ 2.5 $ times the weight of the bob for the position shown, find the velocity and the acceleration of the bob in that position.

(A) $ 16.75m/s,5.66m/{s^2} $
(B) $ 5.66m/s,16.75m/{s^2} $
(C) $ 2.88m/s,16.75m/{s^2} $
(D) $ 5.66m/s,8.34m/{s^2} $

Answer 1

Hint : The tension and the weight are factors affecting the centripetal force required for circular path. Both the radial and tangential acceleration must be considered in calculating the acceleration.

Formula used: In this solution we will be using the following formula;
 $\Rightarrow {F_{NET}} = ma $ where $ {F_{NET}} $ is the net force on a body, $ m $ is the mass of the body, and $ a $ is the acceleration of the body.
 $\Rightarrow {F_c} = \dfrac{{m{v^2}}}{r} $ $ {a_r} = \dfrac{{{v^2}}}{r} $ where $ {a_r} $ is the centripetal acceleration.
 $\Rightarrow {a_t} = g\sin \theta $ where $ {a_t} $ is the tangential acceleration, and $ \theta $ is the angle between the string and the vertical.

Complete step by step answer
To calculate the velocity at that point in the question, we must note that the centripetal force required to move in an arc must be provided by the tension in the string minus the component of the weight in the opposite direction of the tension, hence
 $\Rightarrow T - mg\cos \theta = \dfrac{{m{v^2}}}{r} $ where $ v $ is the velocity, $ m $ is the mass of the bob, and $ r $ is the radius of the arc, in this case the length of the string, and $ \theta $ is the acute angle between the line parallel to tension and the weight of the bob.
Also, the tension is said to be two and a half times the weight of the bob, hence, we get
 $\Rightarrow 2.5mg - mg\cos \theta = \dfrac{{m{v^2}}}{r} $ , by replacing the radius with the length we have
 $\Rightarrow 2.5mg - mg\cos \theta = \dfrac{{m{v^2}}}{l} $ , By cancelling the mass and substituting known values
 $\Rightarrow 2.5\left( {9.8} \right) - 9.8\cos 30^\circ = \dfrac{{{v^2}}}{2} $
By computation,
 $\Rightarrow 24.5 - 8.49 = \dfrac{{{v^2}}}{2} $
Hence,
 $\Rightarrow {v^2} = 2\left( {16.01} \right) = 32.02 $
 $\Rightarrow v = \sqrt {32.02} = 5.66m/s $
For radial acceleration, we have given by
 $\Rightarrow {a_r} = \dfrac{{{v^2}}}{r} $ , hence,
 $\Rightarrow {a_r} = \dfrac{{32.02}}{2} = 16.01m/{s^2} $
For tangential acceleration (acceleration in the direction of the velocity)
 $\Rightarrow {a_t} = g\sin \theta $
Hence, $ {a_t} = 9.8\sin 30^\circ = 4.9m/{s^2} $
Total acceleration is given by
 $\Rightarrow a = \sqrt {{a_r} + {a_t}} $ Hence
 $\Rightarrow a = \sqrt {{{16.01}^2} + {{4.9}^2}} $
By computation, we get
 $\therefore a = 16.75m/{s^2} $
Hence the correct option is B.

Note
Alternatively, after calculating the radial acceleration, an investigation of the options would have revealed the answer. Since, the radial velocity was calculated as $ 16.01m/{s^2} $ , hence, since only increase with a consideration of the tangential acceleration, and the knowledge that velocity is $ 5.66m/s $ , we can conclude that B is the answer without actually calculating the tangential acceleration.